
分析 函数f(x)=$\left\{\begin{array}{l}{1-|x-2|,x∈[1,3]}\\{3f(\frac{x}{3}),x∈(3,+∞)}\end{array}\right.$,可得:x∈[1,2]时,f(x)=x-1∈[0,1];x∈(1,3]时,f(x)=3-x.
当3<x≤9时,则1<$\frac{x}{3}$≤3,由f(x)=3f($\frac{x}{3}$)可知:f(x)∈[0,3].…,依此类推画出函数图象:根据集合P={x|f(x)=m,0<m<1}(m为常数)的元素为xi(i=1,2,3…).其中x1≤x2≤x3≤x4≤….利用对称性与中点坐标公式、等比数列的前n项和公式即可得出.
解答 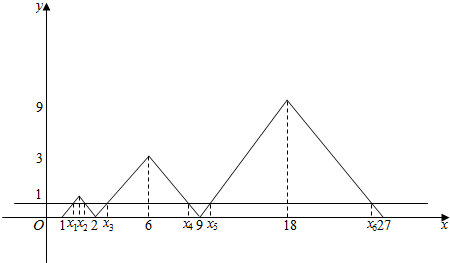 解:∵函数f(x)=$\left\{\begin{array}{l}{1-|x-2|,x∈[1,3]}\\{3f(\frac{x}{3}),x∈(3,+∞)}\end{array}\right.$,
解:∵函数f(x)=$\left\{\begin{array}{l}{1-|x-2|,x∈[1,3]}\\{3f(\frac{x}{3}),x∈(3,+∞)}\end{array}\right.$,
∴x∈[1,2]时,f(x)=x-1∈[0,1];x∈(1,3]时,f(x)=3-x.
当3<x≤9时,则1<$\frac{x}{3}$≤3,由f(x)=3f($\frac{x}{3}$)可知:f(x)∈[0,3].…,
依此类推画出函数图象:
∵集合P={x|f(x)=m,0<m<1}(m为常数)的元素为xi(i=1,2,3…).其中x1≤x2≤x3≤x4≤….
∴当1≤x≤3时,则y=f(x),与y=m有两个交点x1,x2,且x1+x2=2×2=4;
同理,当x∈(0,9]时,则y=f(x),与y=m有两个交点x3,x4,且x3+x4=2×6=4×3;
同理,当x∈(9,27]时,则y=f(x),与y=m有两个交点x5,x6,且x5+x6═2×18=4×32;
….
∴当n∈N*时,x1+x2+x3+x4+…+x2n=4×(1+3+32+…+3n-1)=$4×\frac{{3}^{n}-1}{3-1}$=2(3n-1).
故答案为:2×(3n-1).
点评 本题考查了分段函数的图象与性质、中点坐标公式、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:解答题
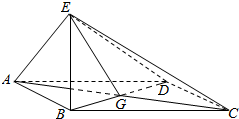 如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{18}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m<\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}<m<\frac{{\sqrt{2}}}{2}$ | C. | $m<-\frac{{\sqrt{2}}}{2}$ | D. | $m>\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4) | B. | (4,+∞) | C. | (-∞,-4$\sqrt{2}$) | D. | (4$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{4}$,+∞) | B. | [$\frac{5}{4}$,+∞) | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
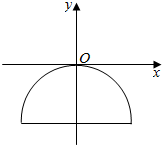 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com