
| A. | [$\frac{3}{4}$,+∞) | B. | [$\frac{5}{4}$,+∞) | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{5}{2}$,+∞) |
分析 根据绝对值的性质得到|x2-ax-a2|=|-x2+ax+a2|≤|-x2+ax|+a2,从而判断出-x2+ax≥0,得到当x=$\frac{a}{2}$时,取到最大值,从而求出m的范围.
解答 解:|x2-ax-a2|=|-x2+ax+a2|≤|-x2+ax|+|a2|=|-x2+ax|+a2,
当且仅当-x2+ax与a2同号时取等号,
故当-x2+ax≥0,有|x2-ax-a2|=-${(x-\frac{a}{2})}^{2}$+$\frac{5}{4}$a2,
当x=$\frac{a}{2}$时,取到最大值$\frac{5}{4}$a2,而|a|≤1,|x|≤1,
∴当a=1,x=$\frac{1}{2}$或a=-1,x=-$\frac{1}{2}$时,
|x2-ax-a2|有最大值$\frac{5}{4}$,
故m≥$\frac{5}{4}$,
故选:B.
点评 本题考察了绝对值的性质,考察求函数的最值问题,是一道中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
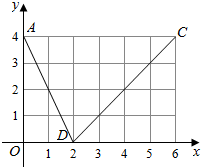 如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )
如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com