
分析 由函数g(x)=x2-2ax的对称轴为x=a,a>1时g(x)在(1,3)上单调递减,且g(x)>0恒成立,0<a<1时g(x)在(1,3)上单调递增,且g(x)>0恒成立,列出不等式求出a的取值范围.
解答 解:由题意得函数g(x)=x2-2ax的对称轴为x=a,
①当a>1时,由复合函数的单调性知,g(x)在(1,3)单调递减,
且g(x)>0在(1,3)上恒成立;
则$\left\{\begin{array}{l}{a>1}\\{g(3)=9-6a>0}\\{a≥3}\end{array}\right.$,
此时a不存在;
②当0<a<1时,由复合函数的单调性知,g(x)在(1,3)单调递增,
且g(x)>0在(1,3)恒成立;
则$\left\{\begin{array}{l}{0<a<1}\\{g(1)=1-2a≥0}\\{a≤1}\end{array}\right.$,
解得0<a≤$\frac{1}{2}$;
综上,a的取值范围是0<a≤$\frac{1}{2}$.
故答案为:(0,$\frac{1}{2}$].
点评 本题主要考查了由对数函数及二次函数的复合函数的单调性问题,解题中一定要注意对数的真数大于0这一条件的考虑,是易错题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:选择题
| A. | $m<\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}<m<\frac{{\sqrt{2}}}{2}$ | C. | $m<-\frac{{\sqrt{2}}}{2}$ | D. | $m>\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{4}$,+∞) | B. | [$\frac{5}{4}$,+∞) | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${3^{\frac{1}{3}}}>{4^{\frac{1}{3}}}$ | B. | 0.30.4>0.30.3 | C. | log76<log67 | D. | sin3>sin2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
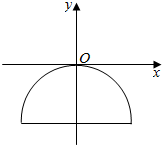 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com