
分析 (1)求出原函数的导函数,由导函数在区间(l,ln 5)上恒大于等于0或恒小于等于0,利用分离参数法求得a的取值范围;
(2)求出函数f(x)的单调区间,求导可知,a<0时g(x)在定义域内为减函数,再由f(x)的减区间非空求得a的范围.
解答 解:(1)f′(x)=ex+a,
∵函数f(x)是(l,ln 5)上的单调函数,
∴f′(x)=ex+a在(l,ln 5)上恒大于等于0或恒小于等于0.
由f′(x)=ex+a≥0,得a≥-ex,
∵当x∈(l,ln 5)时,-ex∈(-5,-e),
∴a∈[-e,0);
由f′(x)=ex+a≤0,得a≤-ex,
∵当x∈(l,ln 5)时,-ex∈(-5,-e),
∴a∈(-∞,-5].
综上,a的取值范围是(-∞,-5]∪[-e,0);
(2)f′(x)=ex+a,令f′(x)=ex+a=0,得x=ln-a,
当x∈(-∞,ln(-a))时,f′(x)<0,当x∈(ln(-a),+∞)时,f′(x)>0.
∴f(x)的减区间为(-∞,ln(-a)),增区间为(ln(-a),+∞);
g′(x)=a-$\frac{1}{x}=\frac{ax-1}{x}$(x>0),
∵a<0,∴g′(x)<0,函数g(x)在(0,+∞)上单调递减.
若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,
则ln(-a)>0,即-a>1,得a<-1.
∴a的取值范围是(-∞,-1).
点评 本题考查利用导数研究函数的单调性,考查导函数的符号与原函数单调性间的关系,是中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:填空题
 已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.
已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {2} | C. | {3,4} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (C${\;}_{8}^{3}$+C${\;}_{7}^{2}$)(C${\;}_{7}^{3}$+C${\;}_{8}^{2}$) | B. | (C${\;}_{8}^{3}$+C${\;}_{7}^{2}$)+(C${\;}_{7}^{3}$+C${\;}_{8}^{2}$) | ||
| C. | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$C${\;}_{8}^{2}$ | D. | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$+C${\;}_{11}^{1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1件正品和恰有1件次品 | B. | 恰有1件次品和至少有1件次品 | ||
| C. | 至少有1件次品和至少有1件正品 | D. | 全部是次品和至少有1件正品 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
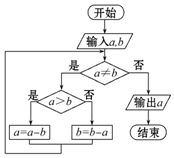 某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( )
某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( )| A. | 0 | B. | 7 | C. | 14 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,$∠ABC=\frac{π}{3}$,且PA⊥平面ABCD.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,$∠ABC=\frac{π}{3}$,且PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com