考点:点、线、面间的距离计算,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(1)M为AA
1中点.取A
1C
1中点N,连结B
1N,MN,B
1M,由已知条件推导出B
1N=
,
B1M=,从而得到
A1M==1,所以M为AA
1中点.
(2)过M作ME⊥BB
1于E,过E作EF⊥B
1C交于F,连MF,由已知条件得∠MFE为二面角M-B
1C-B平面角.由此能求出二面角M-B
1C-C
1的正切值.
(3)过E作EH⊥MF,则EH⊥平面MB
1C,所以EH的长为E到平面MB
1C距离,由此能求出B到平面MB
1C的距离.
解答:
(1)解:M为AA
1中点.
证明如下:取A
1C
1中点N,连结B
1N,MN,B
1M,
∵在直三棱柱ABC-A
1B
1C
1中,AB=BC=1,∠ABC=90°,AA
1=2,
M为棱AA
1上一点,且B
1M与平面ACC
1所成角为30°.
∴B
1N⊥平面ACC
1,∠B
1MN=30°,
∵B
1N=
=
,∴
B1M=,
∴
A1M==1,∴M为AA
1中点.…(4分)
(2)解:过M作ME⊥BB
1于E,
则ME⊥平面BCC
1B
1,且E为BB
1中点,
过E作EF⊥B
1C交于F,连MF,则MF⊥B
1C
∴∠MFE为二面角M-B
1C-B平面角.
在Rt△MEF中,ME=1,EF=
∴tan∠MFE=
=
∴所求二面角M-B
1C-C
1的正切值为
-…(8分)
(3)解:过E作EH⊥MF,则EH⊥平面MB
1C,
∴EH的长为E到平面MB
1C距离,
在Rt△MEF中,EH=
=又∵E为BB
1中点,
∴B到平面MB
1C的距离为2EH=
.…(12分)
点评:本题考查二面角正切值的求法,考查点到平面的距离的求法,解题时要认真审题,注意向量法的合理运用.

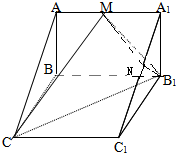
 如图,在直三棱柱ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点,且B1M与平面ACC1所成角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点,且B1M与平面ACC1所成角为30°.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案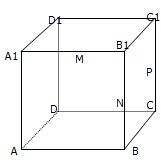 如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.
如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.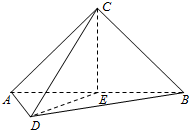 如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2
如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2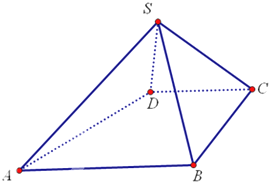 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.