
分析 (Ⅰ)化极坐标方程为普通方程,当a=1时,直接求直线l和曲线C的解得坐标,然后求解弦长|MN|;
(Ⅱ)联立直线与抛物线方程,利用向量的数量积,求解弦长MN,清楚圆心到直线的距离即可求解三角形的面积.
解答 解:(Ⅰ)直线l的极坐标方程为:ρsinθ+ρcosθ=2,直线的普通方程为:x+y=2,
曲线C的极坐标方程为:ρcos2θ=asinθ(a>0),它的普通方程为:ay=x2.当a=1时,
:x2+x-2=0,解得x=1或x=-2,曲线C与直线l的交点为M(-2,4),N
(1,1).
∴|MN|=$\sqrt{9+9}$=3$\sqrt{2}$…(5分)
(Ⅱ)把ay=x2代入可得直线l的普通方程x+y=2消去y得
:x2+ax-2a=0,设M(x1,y1),N(x2,y2),x1+x2=-a,x1x2=-2a,则
y1y2=(-x1+2)(-x2+2)=4∴
$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,∴x1x2+y1y2=-2a+4=0,解得a=2,
此时${x_1}+{x_2}=-2,{x_1}{x_2}=-4,|{x_1}-{x_2}|=\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=2\sqrt{5}$.
|MN|=$\sqrt{2}$|x1-x2|=2$\sqrt{10}$.原点到直线的距离为:h=$\frac{|2|}{\sqrt{2}}$=$\sqrt{2}$.
∴S△0MN=$\frac{1}{2}×\sqrt{2}×2\sqrt{10}$=2$\sqrt{5}$.
点评 本题考试极坐标与普通方程互化,直线与抛物线的位置关系的应用,考查计算能力.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
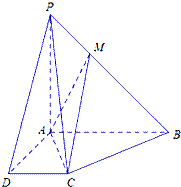 如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
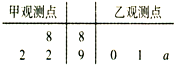 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3<b3 | B. | ab>b2 | C. | ac2>bc2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | 0.4 | 0.9 | 1.1 | 1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -3 | -2 | 0 | 1 | 3 | 4 | 8 |
| f'(x) | -24 | -10 | 6 | 8 | 0 | -10 | -90 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com