
分析 (Ⅰ)由条件和交集的运算求出A∩B,由补集的运算求出∁RA,由并集的运算求出(∁RA)∪B;
(Ⅱ)由并集的运算将B∪C=B转化为C⊆B,根据条件和子集的定义分类讨论,分别列出不等式(组),求出m的取值范围.
解答 解:(Ⅰ)∵集合A={x|x≤-1或x≥3},B={x|1≤x≤6},
∴A∩B={x|3≤x≤6},且∁RA={x|-1<x<3},
∴(∁RA)∪B={x|-1<x≤6}; …(6分)
(Ⅱ)∵B∪C=B,∴C⊆B,
即C={x|m+1≤x≤2m}⊆{x|1≤x≤6},
①当C=∅时,有m+1>2m,解得m<1,
②当C≠∅时,有$\left\{\begin{array}{l}{m+1≤2m}\\{m+1≥1}\\{2m≤6}\end{array}\right.$,解得1≤m≤3,
综上所述:m的取值范围是(-∞,1)∪[1,3],即(-∞,3].…(12分)
点评 本题考查交、并、补集的混合运算,以及集合之间的关系的应用,考查分类讨论思想、转化思想,注意空集是任何集合的子集.


科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1<x≤0} | D. | {x|0≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
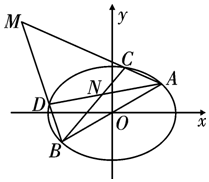 如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点A($\sqrt{2}$,1)是椭圆上的一点,且椭圆C的离心率为$\frac{{\sqrt{2}}}{2}$,直线AO与椭圆C交于点B,且C,D是椭圆上异于A,B的任意两点,直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点A($\sqrt{2}$,1)是椭圆上的一点,且椭圆C的离心率为$\frac{{\sqrt{2}}}{2}$,直线AO与椭圆C交于点B,且C,D是椭圆上异于A,B的任意两点,直线AC,BD相交于点M,直线AD,BC相交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线和直线外一点确定一个平面 | |
| B. | 过不在一条直线上的三点,有且只有一个平面 | |
| C. | 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补 | |
| D. | 平行于同一个平面的两个平面相互平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | $2\sqrt{2}-i$ | D. | $-2\sqrt{2}+i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com