
分析 (1)由题意可得H($\frac{{a}^{2}}{c}$,0),O(0,0),F(c,0),A(a,0)求得|FA|=a-c,|OH|=$\frac{{a}^{2}}{c}$,运用离心率公式可得f(e)=e-e2,配方即可得到所求最大值;
(2)将P的坐标代入椭圆,可得y02=$\frac{{b}^{2}}{{a}^{2}}$(a2-x02)①,再由直线y=kx与圆相切,可得d=r,化简整理可得k的二次方程,运用韦达定理,可得k1k2,代入①,化简整理即可得到定值.
解答 解:(1)由题设,H点的坐标为H($\frac{{a}^{2}}{c}$,0),O(0,0),F(c,0),A(a,0)
∴|FA|=a-c,|OH|=$\frac{{a}^{2}}{c}$,
f(e)=$\frac{|AF|}{|OH|}$=$\frac{a-c}{\frac{{a}^{2}}{c}}$=$\frac{c}{a}$-$\frac{{c}^{2}}{{a}^{2}}$=e-e2=-(e2-e)=-(e-$\frac{1}{2}$)2+$\frac{1}{4}$,
∴当e=$\frac{1}{2}$时,f(e)取得最大值,且为$\frac{1}{4}$;
(2)由点P(x0,y0)是椭圆上任意一点,
可得$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1,即为y02=$\frac{{b}^{2}}{{a}^{2}}$(a2-x02),①
∵直线y=kx与圆相切,
∴d=r,即$\frac{|{y}_{0}-k{x}_{0}|}{\sqrt{1+{k}^{2}}}$=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$,
整理可得(a2b2-x02(a2+b2))k2+2x0y0(a2+b2)k+a2b2-y02(a2+b2)=0,
即有k1k2=$\frac{{a}^{2}{b}^{2}-{{y}_{0}}^{2}({a}^{2}+{b}^{2})}{{a}^{2}{b}^{2}-{{x}_{0}}^{2}({a}^{2}+{b}^{2})}$,
代入①,化简可得k1k2=-$\frac{{b}^{2}}{{a}^{2}}$.
点评 本题考查椭圆的方程和性质及运用,考查两点的距离公式的运用和二次函数的最值的求法,考查直线和圆相切的条件:d=r,以及化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 27 | C. | 37 | D. | 212 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
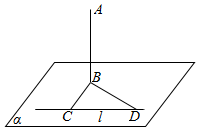 如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com