
 某算法的程序框图如图所示,其中输入的变量x在1,&2,&3,&…,&24这24个整数中等可能随机产生.分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3).
某算法的程序框图如图所示,其中输入的变量x在1,&2,&3,&…,&24这24个整数中等可能随机产生.分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3). 分析 模拟程序的运行,可得程序框图的功能是计算y=$\left\{\begin{array}{l}{\stackrel{1}{2}}&{\stackrel{x不是偶数}{x是偶数但不能被3整除}}\\{3}&{x是偶数但能被3整除}\end{array}\right.$的值,用列举法写出结果,即可求得概率.
解答 (本题满分为10分)
解:模拟程序的运行,可得:
x的值为:1,3,5,7,9,11,13,15,17,19,21,23时,y=1,
所以:${P_1}=\frac{12}{24}=\frac{1}{2}$.…4分
x的值为:2,4,8,10,14,16,20,22时,y=2,
所以:${P_2}=\frac{8}{24}=\frac{1}{3}$.…7分
x的值为:6,12,18,24时,y=3,
所以:${P_3}=\frac{4}{24}=\frac{1}{6}$.…10分
点评 本题主要考查程序框图的识别和运行,根据条件分别进行运行即可得到结论,考查了分类讨论思想,属于基础题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
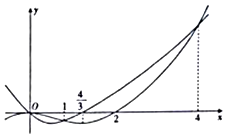
| A. | (0,4) | B. | $({-∞,1}),({\frac{4}{3},4})$ | C. | $({0,\frac{4}{3}})$ | D. | (0,1),(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+$\frac{1}{a}$>2 | B. | a+$\frac{1}{a}$≥2 | C. | a+$\frac{1}{a}$≤-2 | D. | |a+$\frac{1}{a}$|≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}3-{x^2},x∈[-1,2]\\ x-3,x∈(2,5].\end{array}$
已知函数f(x)=$\left\{\begin{array}{l}3-{x^2},x∈[-1,2]\\ x-3,x∈(2,5].\end{array}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<3} | B. | {x|1≤x<3} | C. | {0,1,2} | D. | {1,2,3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com