
分析 (I)利用等差数列与等比数列的通项公式可得an,Sn,再利用递推关系可得bn.
(II)利用“裂项求和”方法即可得出.
解答 解:(I)设{an}的公比为q(q>0),则$\left\{{\begin{array}{l}{{a_1}{q^2}-{a_1}=\frac{16}{27}}\\{{a_1}q=-\frac{2}{9}}\end{array}}\right.$,
∴3q2+8q-3=0,由q>0,解得$q=\frac{1}{3}$,${a_1}=-\frac{2}{3}$,
∴${a_n}=-2×{({\frac{1}{3}})^n}$.
∵${S_n}-{S_{n-1}}=({\sqrt{S_n}+\sqrt{{S_{n-1}}}})({\sqrt{S_n}-\sqrt{{S_{n-1}}}})$=$\sqrt{S_n}+\sqrt{{S_{n-1}}}$,
又bn>0,$\sqrt{S_n}>0$,∴$\sqrt{S_n}-\sqrt{{S_{n-1}}}=1$,数列$\left\{{\sqrt{S_n}}\right\}$构成一个公差为1的等差数列,
∵$\sqrt{{S_{10}}}=10$,∴S1=1,∴$\sqrt{S_n}=n$,${S_n}={n^2}$.
当n=1,b1=S1=1,
当n≥2,bn=Sn-Sn-1=2n-1(n=1也满足).
(II)$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴Tn=$\frac{1}{2}[(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$=$\frac{1}{2}(1-\frac{1}{2n+1})$.
∴${T_n}=\frac{n}{2n+1}$.
点评 本题考查了“裂项求和法”、等差数列与等比数列的通项公式及其求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | logab•logbc•logca=1 | B. | 函数f(x)=ex满足f(a+b)=f(a)•f(b) | ||
| C. | 函数f(x)=ex满足f(a•b)=f(a)•f(b) | D. | 若xlog34=1,则4x+4-x=$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
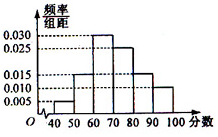 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )| A. | 588 | B. | 480 | C. | 450 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com