
(本小题满分14分)已知关于x的函数 .
.
(I)求函数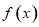 在点
在点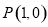 处的切线方程;
处的切线方程;
(II)求函数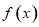 有极小值,试求a的取值范围;
有极小值,试求a的取值范围;
(III)若在区间 上,函数
上,函数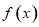 不出现在直线
不出现在直线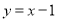 的上方,试求a的最大值.
的上方,试求a的最大值.
(Ⅰ)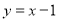 (Ⅱ)
(Ⅱ)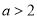 (III)
(III)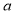 的最大值为0.
的最大值为0.
【解析】
试题分析:(Ⅰ)求导,利用导数的几何意义进行求解;(Ⅱ)求导,讨论二次方程的二次项系数的符号与两根的大小进行求解;(III)构造函数,将问题转化为不等式恒成立,利用导数求最值即可.
试题解析:(Ⅰ)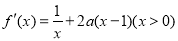
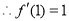
又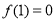
所以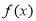 在点P(1,0)处的切线方程为
在点P(1,0)处的切线方程为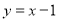 . 4分
. 4分
(Ⅱ)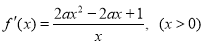 5分
5分
令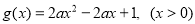
(i)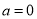 时
时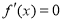 无解,
无解,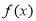 无极小值;
无极小值;
(ii) 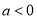 时,
时,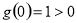 ,所以
,所以 有两解
有两解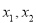 ,且
,且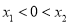 ;
;
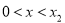 时
时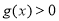 ,
,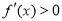
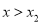 时
时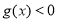 ,
,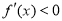
此时,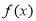 无极小值. 7分
无极小值. 7分
(iii) 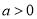 时, 因为
时, 因为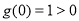 ,
,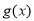 的对称轴为
的对称轴为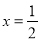 ,要使函数
,要使函数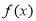 有极小值,则
有极小值,则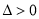 即
即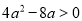
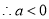 或
或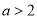
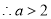
此时 有两解
有两解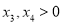 ,不妨设设
,不妨设设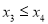 , 则
, 则 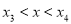 时
时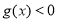 ,
,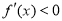
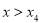 时
时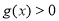 ,
,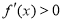 此时,
此时,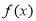 有极小值
有极小值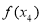 . 9分
. 9分
综上所述,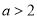 . 10分
. 10分
(Ⅲ)由题意,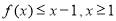
即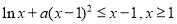 11分
11分
下证: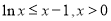
记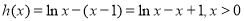
则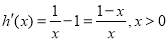
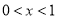 时
时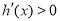 ,
,
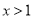 时
时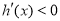 ,
,
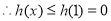
即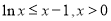 12分
12分
(i) 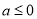 时,
时,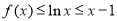
(ii) 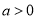 时,取
时,取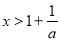 ,
,
则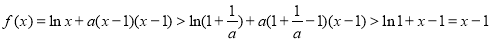
与题意矛盾.
故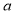 的最大值为0.
的最大值为0.
考点:1.导数的几何意义;2.函数的极值与最值;3.分类讨论思想.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:2014-2015学年山东省青岛市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
若圆台两底面周长的比是1:4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是
A.1:16 B.39:129 C.13:129 D.3:27
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省无锡市高三上学期期末考试理科数学试卷(解析版) 题型:填空题
将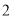 本不同的数学书和
本不同的数学书和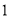 本语文书在书架上随机排成一行,则
本语文书在书架上随机排成一行,则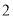 本数学书相邻的概率为
本数学书相邻的概率为
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省信阳市毕业班第二次调研检测文科数学试卷(解析版) 题型:选择题
已知函数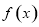 的定义域为
的定义域为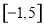 ,部分对应值如下表,
,部分对应值如下表,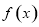 的导函数y=
的导函数y=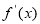 的图象如图所示.
的图象如图所示.
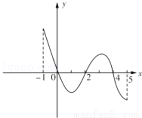
x | -1 | 0 | 2 | 4 | 5 |
y | 1 | 2 | 0 | 2 | 1 |
若函数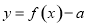 有
有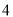 个零点,则实数
个零点,则实数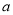 的取值范围为( )
的取值范围为( )
(A)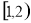 (B)
(B)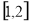 (C)
(C) 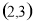 (D)
(D)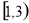
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省信阳市毕业班第二次调研检测文科数学试卷(解析版) 题型:选择题
在“信阳市中学生歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )

(A)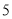 和
和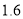 (B)
(B)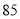 和
和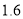 (C)
(C) 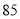 和
和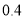 (D)
(D) 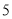 和
和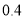
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省济南市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在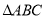 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为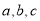 ,且
,且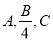 成等差数列.
成等差数列.
(I)若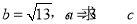 的值;
的值;
(II)设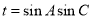 ,求t的最大值.
,求t的最大值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省南昌市高三上学期第四次月考理科数学试卷(解析版) 题型:填空题
若实数 满足
满足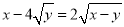 ,则
,则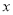 的取值范围是____________________.
的取值范围是____________________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三下学期期初开学联考理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=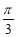 ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com