
���� ��1������Ϊ�ң�����ͬ�˦ѣ���Ϲ�ʽx=��cos�ȣ�y=��sin�ȿɵ�����C��ֱ�����귽�̣�ֱ�ǰ�ֱ��l�IJ���������ȥ����t�ɵ�����ͨ���̣�
��2������ֱ�߷����������߷��̣����M��N�ĺ����꣬��|PM|=|MN|ת��Ϊ������Ĺ�ϵ��mֵ��
��� �⣺��1���ɦ�•sin��•tan��=4m���æ�sin2��=4mcos�ȣ�����2sin2��=4m��cos�ȣ�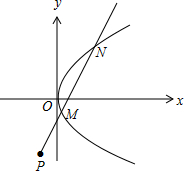
��y2=4mx��m��0����
������C��ֱ�����귽��Ϊy2=4mx��m��0����
��$\left\{{\begin{array}{l}{x=-1+tcos{{45}��}}\\{y=-2+tsin{{45}��}}\end{array}}\right.$����$\left\{\begin{array}{l}{x=-1+\frac{\sqrt{2}}{2}t}\\{y=-2+\frac{\sqrt{2}}{2}t}\end{array}\right.$����
��ȥ����t�ã�x-y-1=0��
��ֱ��l����ͨ����Ϊx-y-1=0��
��2����ͼ������$\left\{\begin{array}{l}{y=x+1}\\{{y}^{2}=4mx}\end{array}\right.$����x2+��2-4m��x+1=0��
��ã�${x}_{1}=2m-1-2\sqrt{{m}^{2}-m}$��${x}_{2}=2m-1+2\sqrt{{m}^{2}-m}$��
������ɵã�$2m-1-2\sqrt{{m}^{2}-m}+1$=$4\sqrt{{m}^{2}-m}$�����m=$\frac{9}{8}$��m��0����
���� ���⿼��������̻���ͨ���̣������˼����ߵļ����귽�̣����������ν�ϵĽ���˼�뷽�������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
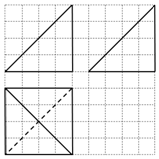 ij�ռ伸���������ͼ��ͼ��ʾ��ͼ��С�����εı߳�Ϊ1��������������������ǣ�������
ij�ռ伸���������ͼ��ͼ��ʾ��ͼ��С�����εı߳�Ϊ1��������������������ǣ�������| A�� | 16 | B�� | 32 | C�� | $\frac{64}{3}$ | D�� | $\frac{32}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m�Φ���n�ͦ��Ҧ��ͦ£���m��n | B�� | ��m�ͦ���n�ͦ��Ҧ��ͦ£���m��n | ||
| C�� | �����ͦ£����ɦ�=m��n��m����n�ͦ� | D�� | �����ɦ�=m��n?����m��n������ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\frac{5}{2}$ | C�� | $\frac{7}{2}$ | D�� | $\frac{7}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com