
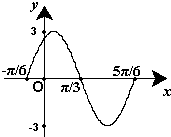
 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.分析 (1)由函数的图象的顶点坐标求出A,由特殊点的坐标求出φ的值,再根据五点法作图求出ω的值,从而求得该函数的解析式;
(2)由$0≤x≤\frac{π}{2}$,得$\frac{π}{3}≤2x+\frac{π}{3}≤\frac{4π}{3}$,即可得出结论.
解答 解:(1)由图可知A=3,T=$\frac{5π}{6}-(-\frac{π}{6})$=π,又$T=\frac{2π}{ω}$,故ω=2…3
所以y=3sin(2x+φ),把$(-\frac{π}{6},0)$代入得:$0=3sin(-\frac{π}{3}+φ)$
故$-\frac{π}{3}+φ=2kπ$,∴$φ=2kπ+\frac{π}{3}$,k∈Z
∵|φ|<π,故k=1,$φ=\frac{π}{3}$,∴$f(x)=3sin(2x+\frac{π}{3})$…5
(2)∵$0≤x≤\frac{π}{2}$,∴$\frac{π}{3}≤2x+\frac{π}{3}≤\frac{4π}{3}$,…7
当$2x+\frac{π}{3}=\frac{π}{2}$,即$x=\frac{π}{12}$时,函数f(x)取得最大值3;…9
当$2x+\frac{π}{3}=\frac{4π}{3}$,即$x=\frac{π}{2}$时,函数f(x)取得最小值是$-\frac{{3\sqrt{3}}}{2}$…12
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由特殊点的坐标求出φ的值,再根据五点法作图求出ω的值,属于中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 虚数集和各个象限内的点的集合是一一对应的 | |
| B. | 实、虚部都是负数的虚数的集合与第二象限的点的集合是一一对应的 | |
| C. | 实部是负数的复数的集合与第二、三象限的点的集合是一一对应的 | |
| D. | 实轴上侧的点的集合与虚部为正数的复数的集合是一一对应的 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x>1,则x2>1”的逆命题 | B. | 命题“若x=1,则x2+x-2=0”的否命题 | ||
| C. | 命题“若x>y,则x>|y|”的逆命题 | D. | 命题“若x2>0,则x>-1”的逆否命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com