
分析 如果命题“p∧q”为假命题,则命题p为假,或命题q为假,进而得到实数m的取值范围.
解答 解:若函数f(x)=x3+mx2+(m+$\frac{4}{3}$)x+6在R有极值;
则函数f′(x)=3x2+2mx+(m+$\frac{4}{3}$)的△=$4{m}^{2}-12(m+\frac{4}{3})>0$,
解得:m<-1,或m>4,
即命题p:m<-1,或m>4,
3x-9x<m,即3x-(3x)2<m,即t-t2<m(t>0),
即m>$\frac{1}{2}$,
即命题q:m>$\frac{1}{2}$,
果命题“p∧q”为假命题,
则命题p为假,或命题q为假,
即:-1≤m≤4,或m≤$\frac{1}{2}$,
即m≤4.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,利用导数研究函数的极值,函数恒成立问题等知识点,难度中档.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x,g(x)={(\sqrt{x})^2}$ | B. | $f(x)=\left|x\right|,g(x)=\sqrt{[}3]{x^3}$ | ||
| C. | $f(x)={x^2},g(x)=\left\{\begin{array}{l}{x^2},(x>0)\\-{x^2},(x<0)\end{array}\right.$ | D. | $f(x)=\frac{{{x^2}-1}}{x-1},g(t)=t+1(t≠1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
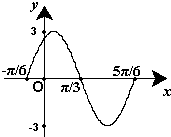 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
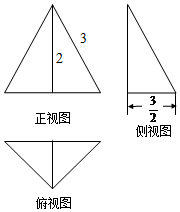
| A. | 12π | B. | $6\sqrt{3}π$ | C. | 9π | D. | 18π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com