
分析 (1)由|AF1|=$\sqrt{5}$求得c,结合椭圆离心率求得a,进一步求得b,则椭圆方程可求;
(2)由题意可知,直线l的斜率存在,设直线方程为y=kx+1.由$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,得(5+9k2)x2+18kx-36=0.设M(x1,y1),N(x2,y2),再利用根与系数关系结合3$\overrightarrow{AM}$+2$\overrightarrow{AN}$=$\overrightarrow 0$得到k值,由此能求出直线l的方程.
解答 解:(1)由|AF1|=$\sqrt{5}$,得c2+1=5,解得c=2.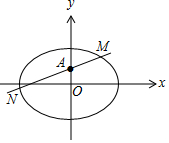
又$e=\frac{c}{a}=\frac{2}{3}$,∴a=3,则b2=a2-c2=5.
∴椭圆C的标准方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$;
(2)由题意可知,直线l的斜率存在,设直线方程为y=kx+1,
联立$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,得(5+9k2)x2+18kx-36=0.
设M(x1,y1),N(x2,y2),
则${x}_{1}+{x}_{2}=-\frac{18k}{5+9{k}^{2}},{x}_{1}{x}_{2}=-\frac{36}{5+9{k}^{2}}$,①
由3$\overrightarrow{AM}$+2$\overrightarrow{AN}$=$\overrightarrow 0$,得$\overrightarrow{AM}=-\frac{2}{3}\overrightarrow{AN}$,
∴(x1,y1-1)=$-\frac{2}{3}({x}_{2},{y}_{2}-1)$,则${x}_{1}=-\frac{2}{3}{x}_{2}$,②
把②代入①得:5+9k2=54k2,解得k=$±\frac{1}{3}$.
∴直线l的方程为$y=±\frac{1}{3}x+1$.
点评 本题考查用待定系数法求曲线方程的能力,通过处理直线与圆锥曲线的位置关系,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
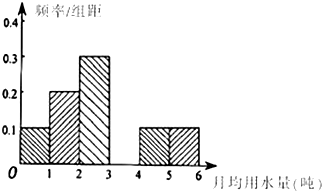 为了解某市居民日常用水量的标准,某机构通过抽样获得了100位居民某年的月均用水量(单位:吨),如表是这100位居民月均用水量的频率分布表,根据如表解答下列问题:
为了解某市居民日常用水量的标准,某机构通过抽样获得了100位居民某年的月均用水量(单位:吨),如表是这100位居民月均用水量的频率分布表,根据如表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | b |
| [1,2) | 20 | 0.20 |
| [2,3) | a | 0.30 |
| [3,4) | 20 | 0.20 |
| [4,5) | 10 | 0.10 |
| [5,6] | 10 | 0.10 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2π}{3}$,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{4π}{3}$] | C. | [-$\frac{5π}{3}$,-$\frac{2π}{3}$] | D. | [0,π] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com