
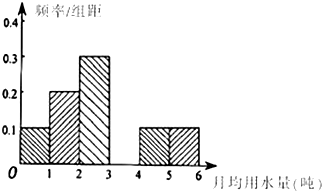
 为了解某市居民日常用水量的标准,某机构通过抽样获得了100位居民某年的月均用水量(单位:吨),如表是这100位居民月均用水量的频率分布表,根据如表解答下列问题:
为了解某市居民日常用水量的标准,某机构通过抽样获得了100位居民某年的月均用水量(单位:吨),如表是这100位居民月均用水量的频率分布表,根据如表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | b |
| [1,2) | 20 | 0.20 |
| [2,3) | a | 0.30 |
| [3,4) | 20 | 0.20 |
| [4,5) | 10 | 0.10 |
| [5,6] | 10 | 0.10 |
| 合计 | 100 | 1.00 |
分析 (1)利用频数之和等于样本容量求出a处的数;利用频率分布表得出第一组的频数为10,求出b处的数;
(2)根据各小组的频率比即频率分布直方图的高度比即可补全频率分布直方图;设所求中位数为x,则0.1+0.2+(x-2)×0.3=0.5,即可得出结论.
解答 解:(1)由频率分布表得出第二小组的频率为:0.03,a=30; …(2分)
由频率分布表得出第一组的频数为10,频率为b=0.10.…(4分)
(2)频率分布直方图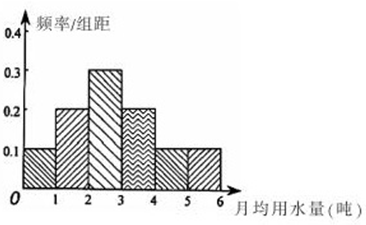
设所求中位数为x,则0.1+0.2+(x-2)×0.3=0.5,
解得:x≈2.67(吨)
答:估计该市每位居民月均用水量的中位数为2.67吨.
点评 用样本估计总体,是研究统计问题的一个基本思想方法.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-2,-1) | C. | (-2,-1] | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该命题的逆命题为真,逆否命题也为真 | |
| B. | 该命题的逆命题为真,逆否命题也假 | |
| C. | 该命题的逆命题为假,逆否命题为真 | |
| D. | 该命题的逆命题为假,逆否命题也为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x,g(x)={(\sqrt{x})^2}$ | B. | $f(x)=\left|x\right|,g(x)=\sqrt{[}3]{x^3}$ | ||
| C. | $f(x)={x^2},g(x)=\left\{\begin{array}{l}{x^2},(x>0)\\-{x^2},(x<0)\end{array}\right.$ | D. | $f(x)=\frac{{{x^2}-1}}{x-1},g(t)=t+1(t≠1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com