练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．命题“若c＜0，则方程x2+x+c=0有实数解”，则（　　）
    A．该命题的逆命题为真，逆否命题也为真
    B．该命题的逆命题为真，逆否命题也假
    C．该命题的逆命题为假，逆否命题为真
    D．该命题的逆命题为假，逆否命题也为假

    分析 利用四种命题题的定义、一元二次方程的实数根与判别式的关系即可判断出．

    解答 解：命题“若c＜0，则方程x2+x+c=0有实数解，即原命题为真命题，
    则其逆否命题也为真，
    其逆命题为：方程x2+x+c=0有实数解，则c＜0，
    若方程x2+x+c=0有实数解，则1-4c≥0，解得c≤$\frac{1}{4}$．故逆命题为假，
    则其否命题也为假，
    故选：C

    点评 本题考查了的逆否关系以及真假判断，是基础题，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知等差数列{an}的前n项和为Sn，若S5=8，S10=20，则S15等于（　　）
    A．16B．18C．36D．38

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．幂函数y=f（x）的图象过点$（{\sqrt{2}，\frac{1}{2}}）$，则其解析式为y=x-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．函数y=log5x+2（x≥1）的值域是（　　）
    A．RB．[2，+∞）C．[3，+∞]D．（-∞，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的个数是．（　　）
    ①若ab＞c2，则$C＜\frac{π}{3}$
    ②若a+b＞2c，则$C＜\frac{π}{3}$
    ③若a3+b3=c3，则$C＜\frac{π}{2}$
    ④若（a+b）c＜2ab，则$C＞\frac{π}{2}$
    ⑤若（a2+b2）c2＜2a2b2，则$C＞\frac{π}{3}$．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知点D（x0，y0）为椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上一点，直线l：xx0+yy0=2a与直线x=±2分别交于G、H两点，且$\overrightarrow{OG}•\overrightarrow{OH}$=-2（其中O为坐标原点），则椭圆E的离心率为$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

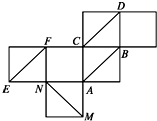
    1．如图是棱长为1的正方体的平面展开图，则在这个正方体中，以下结论错误的是（　　）
    A．点M到AB的距离为$\frac{{\sqrt{2}}}{2}$B．AB与EF所成角是90°
    C．三棱锥C-DNE的体积是$\frac{1}{6}$D．EF与MC是异面直线

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

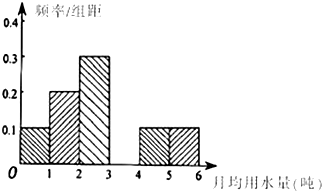    18．为了解某市居民日常用水量的标准，某机构通过抽样获得了100位居民某年的月均用水量（单位：吨），如表是这100位居民月均用水量的频率分布表，根据如表解答下列问题：
    （1）求如表中a和b的值；
    （2）请将下面的频率分布直方图补充完整，并根据直方图估计该市每位居民月均用水量的中位数（精确到0.01）．
    分组频数频率
    [0，1）10b
    [1，2）200.20
    [2，3）a0.30
    [3，4）200.20
    [4，5）100.10
    [5，6]100.10
    合计1001.00

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

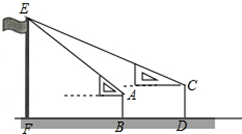    19．某校高一年级某班开展数学活动，小李和小军合作用一副三角板测量学校的旗杆，小李站在B点测得旗杆顶端E点的仰角为45°，小军站在点D测得旗杆顶端E点的仰角为30°，已知小李和小军相距（BD）6米，小李的身高（AB）1.5米，小军的身高（CD）1.75米，求旗杆的高EF的长．（结果精确到0.1，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    同步练习册答案