
分析 首先利用降幂公式及辅助角公式化简.
(1)直解把x=$\frac{π}{8}$代入函数解析式化简求值;
(2)由x的范围求出相位的范围,进一步得到函数的值域,结合f(x)≥t-$\frac{12}{t}$恒成立,转化为关于t的不等式求解;
(3)由x∈[0,a]得到2x-$\frac{π}{4}$∈[$-\frac{π}{4},2a-\frac{π}{4}$],再由函数的值域得到$sin(2x-\frac{π}{4})$∈[-$\frac{\sqrt{2}}{2},1$],从而得到$\frac{π}{2}≤2a-\frac{π}{4}≤\frac{5π}{4}$,由此可得a的范围.
解答 解:f(x)=sinx(sinx+cosx)=sin2x+sinxcosx
=$\frac{1-cos2x}{2}+\frac{1}{2}sin2x$=$\frac{1}{2}(sin2x-cos2x)+\frac{1}{2}$=$\frac{\sqrt{2}}{2}sin(2x-\frac{π}{4})+\frac{1}{2}$.
(1)f($\frac{π}{8}$)=$\frac{\sqrt{2}}{2}sin(2×\frac{π}{8}-\frac{π}{4})+\frac{1}{2}=\frac{1}{2}$;
(2)∵x∈[$\frac{π}{4}$,$\frac{5π}{12}$],∴2x$-\frac{π}{4}$∈[$\frac{π}{4},\frac{7π}{12}$],
则sin(2x-$\frac{π}{4}$)∈[$\frac{\sqrt{2}}{2},1$],f(x)∈[1,$\frac{\sqrt{2}+1}{2}$],
由f(x)≥t-$\frac{12}{t}$恒成立,得$t-\frac{12}{t}≤1$,解得:-3≤t≤4;
(3)由x∈[0,a],得2x-$\frac{π}{4}$∈[$-\frac{π}{4},2a-\frac{π}{4}$],
∵函数f(x)在[0,a]上的值域为[0,$\frac{1+\sqrt{2}}{2}$],
则$\frac{\sqrt{2}}{2}sin(2x-\frac{π}{4})∈$[-$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$],即$sin(2x-\frac{π}{4})$∈[-$\frac{\sqrt{2}}{2},1$].
则$\frac{π}{2}≤2a-\frac{π}{4}≤\frac{5π}{4}$,解得:$\frac{3π}{8}≤a≤\frac{3π}{4}$.
∴实数a的取值范围是[$\frac{3π}{8},\frac{3π}{4}$].
点评 本题考查了三角函数最值的求法,考查了函数恒成立问题,考查了数学转化思想方法,考查了计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,2) | C. | (2,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
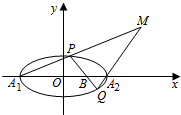 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com