
���� ��I��������ɵ�A��-a��0����B��0��b�������AB��б�ʺͷ��̣����õ㵽ֱ�ߵľ��빫ʽ�ⷽ�̿ɵ�a��b�������õ���Բ���̣�
�������۵�ֱ��l��б�ʲ����ں�Ϊ0����Ϊ0�����ֱ��l�ķ���Ϊy=kx+t��������Բ���̿ɵã�1+6k2��x2+12ktx+6t2-6=0������Τ�ﶨ�����е����깫ʽ������ֱ�ߵļнǹ�ʽ����ϻ�������ʽ���ɵ���Сֵ����ֱ�ߺ�Բ���е�������d=r�������õ�ֱ�߷��̣�
��� �⣺��I��������ɵ�A��-a��0����B��0��b����
kAB=$\frac{b}{a}$=$\frac{\sqrt{6}}{6}$��
ֱ��AB�ķ���Ϊy=$\frac{\sqrt{6}}{6}$x+b��
������ɵ�$\frac{b}{\sqrt{1+\frac{1}{6}}}$=$\frac{\sqrt{42}}{7}$��
���b=1��a=$\sqrt{6}$��
������Բ�ķ���Ϊ$\frac{{x}^{2}}{6}$+y2=1��
����ֱ��l��б�ʲ�����ʱ������OM��l���н�Ϊ90�㣻
��ֱ��l��б��Ϊ0ʱ�����������⣻
��ֱ��l�ķ���Ϊy=kx+t��������Բ���̿ɵ�
��1+6k2��x2+12ktx+6t2-6=0��
�ɵ�x1+x2=-$\frac{12kt}{1+6{k}^{2}}$��
�ɵ��е�M��-$\frac{6kt}{1+6{k}^{2}}$��$\frac{t}{1+6{k}^{2}}$����
��ֱ��l��Բx2+y2=1���У��ɵ�
$\frac{|t|}{\sqrt{1+{k}^{2}}}$=1����1+k2=t2��
�ɵ�OM��б��Ϊk'=-$\frac{1}{6k}$��
ֱ��l��OM�ļнǵ�����Ϊ��$\frac{-\frac{1}{6k}-k}{1-\frac{1}{6k}•k}$|=$\frac{6}{5}$|-k-$\frac{1}{6k}$|��
��k��0ʱ��-k-$\frac{1}{6k}$��2$\sqrt{��-k��•��-\frac{1}{6k}��}$=$\frac{\sqrt{6}}{3}$��
��k=-$\frac{\sqrt{6}}{6}$ʱ���н�ȡ����Сֵ��
���t2=$\frac{7}{6}$�����t=��$\frac{\sqrt{42}}{6}$��
�ɵ�ֱ��l�ķ���Ϊy�T-$\frac{\sqrt{6}}{6}$x��$\frac{\sqrt{42}}{6}$��
��k��0ʱ���ɵ�k=$\frac{\sqrt{6}}{6}$ʱ���н�ȡ����Сֵ��
���t2=$\frac{7}{6}$�����t=��$\frac{\sqrt{42}}{6}$��
�ɵ�ֱ��l�ķ���Ϊy�T��$\frac{\sqrt{6}}{6}$x��$\frac{\sqrt{42}}{6}$��
ʹ��l��ֱ��0M�ļнǴﵽ��С��
���� ���⿼����Բ�ķ��̵���ע������ֱ�ߵ�б�ʹ�ʽ�͵㵽ֱ�ߵľ��빫ʽ��������ֱ�нǵ���ֵ����ע�����üнǹ�ʽ��ͬʱ����ֱ�߷��̺���Բ��������������Τ�ﶨ�����е����깫ʽ���������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | $\sqrt{5}$ | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
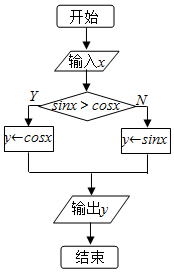 ��ͼ��ʾ������ͼ���������x��ֵΪ$\frac{��}{3}$������Ӧ�����yֵΪ$\frac{1}{2}$��
��ͼ��ʾ������ͼ���������x��ֵΪ$\frac{��}{3}$������Ӧ�����yֵΪ$\frac{1}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
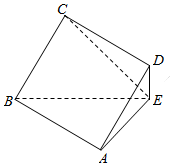 ��ͼ���ı���ABCD�������Σ�DE��ƽ��ABE��BE=3DE��DE=3��AB��AE��
��ͼ���ı���ABCD�������Σ�DE��ƽ��ABE��BE=3DE��DE=3��AB��AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
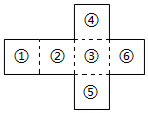 ��ͼ��һ��������ֽ�е�չ��ͼ���Ѹ���1��-1��2i��-2i��$\sqrt{2}$��-$\sqrt{2}$�����߷ֱ��������������۳��������������ϵ���������ģ��ȣ���ͬ�����48�֣�����������
��ͼ��һ��������ֽ�е�չ��ͼ���Ѹ���1��-1��2i��-2i��$\sqrt{2}$��-$\sqrt{2}$�����߷ֱ��������������۳��������������ϵ���������ģ��ȣ���ͬ�����48�֣������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | Ƶ�� | Ƶ�� |
| ��49.5��59.5�� | 12 | 0.24 |
| ��59.5��69.5�� | 16 | 0.32 |
| ��69.5��79.5�� | 10 | |
| ��79.5��89.5�� | 0.16 | |
| ��89.5��99.5�� | ||
| �ϼ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com