
分析 (1)由题意,b=1,$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,求出a,b,即可求椭圆C的方程;
(2)讨论直线l的斜率不存在,设出直线l的方程,求得圆的方程,求得定点T,讨论直线l的斜率存在,设出直线方程,联立椭圆方程,运用韦达定理和圆的性质,结合向量垂直的条件,即可得到存在定点T.
解答 解:(1)由题意,b=1,$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
∴a=2,b=1,c=1,
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1;
(2)①当直线l的斜率不存在时,以AB为直径的圆的方程为:x2+y2=1
②当直线l的斜率为0时,直线l的方程为y=m,
此时以AB为直径的圆的方程为:x2+(y-m)2=2(1-m)2,与x2+y2=1联立,得y=$\frac{3{m}^{2}-1}{2m}$,
∵(x,$\frac{3{m}^{2}-1}{2m}$)在椭圆上,
∴$\frac{3{m}^{2}-1}{2m}$=1,
∵-1<m<0,∴m=-$\frac{1}{3}$,
∴m=-$\frac{1}{3}$,在椭圆上可能存在定点T(0,1)满足条件;
③斜率存在时,设直线l的方程为:y=kx-$\frac{1}{3}$,A(x1,y1),B(x2,y2),
与椭圆方程联立,可得(1+2k2)x2-$\frac{4}{3}$kx-$\frac{16}{9}$=0,
∴x1+x2=$\frac{4k}{3(1+2{k}^{2})}$,x1x2=-$\frac{16}{9(1+2{k}^{2})}$,
$\overrightarrow{TA}•\overrightarrow{TB}$=(k2+1)x1x2-$\frac{4}{3}$k(x1+x2)+$\frac{16}{9}$=(k2+1)(-$\frac{16}{9(1+2{k}^{2})}$)-$\frac{4}{3}$k•$\frac{4k}{3(1+2{k}^{2})}$+$\frac{16}{9}$=0,
∴过M(0,-$\frac{1}{3}$)的直线l斜率存在时,以AB为直径的圆过定点T(0,1),
综上所述,m=-$\frac{1}{3}$时,过M(0,-$\frac{1}{3}$)的直线无论如何转动,以AB为直径的圆过定点T(0,1).
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的运用,联立直线方程和椭圆方程,运用韦达定理,同时考查直线和圆的位置关系,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
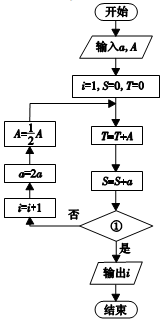 我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:| A. | T>2S? | B. | S>2T? | C. | S<2T? | D. | T<2S? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 504 | C. | 1008 | D. | 2016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com