
Ζ÷Έω ΫΪ$\overrightarrow a•Θ®\overrightarrow b-\overrightarrow aΘ©=-4$’ΙΩΣΩ…ΒΟ$\overrightarrow{a}•\overrightarrow{b}$Θ§ΫΪ|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{7}$ΝΫ±ΏΤΫΖΫΩ…«σ≥ω|$\overrightarrow{b}$|Θ§‘Ό¥ζ»κœρΝΩΒΡΦ–Ϋ«ΙΪ ΫΦΤΥψΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚΓΏ$\overrightarrow{a}Θ®\overrightarrow{b}-\overrightarrow{a}Θ©$=$\overrightarrow{a}•\overrightarrow{b}-{\overrightarrow{a}}^{2}$=-4Θ§${\overrightarrow{a}}^{2}$=|$\overrightarrow{a}$|2=1Θ§
Γύ$\overrightarrow{a}•\overrightarrow{b}$=-3Θ°
ΓΏ|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{7}$Θ§Φ¥${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=7Θ§
Γύ${\overrightarrow{b}}^{2}$=12Θ§Φ¥|$\overrightarrow{b}$|=2$\sqrt{3}$Θ°
ΓύcosΘΦ$\overrightarrow{a}Θ§\overrightarrow{b}$ΘΨ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{\sqrt{3}}{2}$Θ°
ΓΏ0ΓήΘΦ$\overrightarrow{a}Θ§\overrightarrow{b}$ΘΨΓήΠ–Θ§
ΓύΘΦ$\overrightarrow{a}Θ§\overrightarrow{b}$ΘΨ=$\frac{5Π–}{6}$Θ°
Ι ¥πΑΗΈΣΘΚ$\frac{5Π–}{6}$Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΤΫΟφœρΝΩΒΡ ΐΝΩΜΐ‘ΥΥψΘ§ τ”ΎΜυ¥ΓΧβΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2 | BΘ° | 3 | CΘ° | $\sqrt{2}$ | DΘ° | $\sqrt{3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
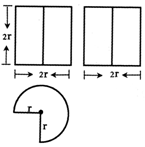
| AΘ° | 18Π–+16 | BΘ° | 20Π–+16 | CΘ° | 22Π–+16 | DΘ° | 24Π–+16 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
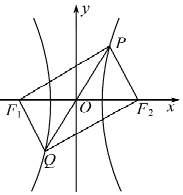 “―÷ΣF1Θ§F2 «ΥΪ«ζœΏCΘΚ$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1Θ®aΘΨ0$Θ§bΘΨ0Θ©ΒΡΉσΓΔ”“ΫΙΒψΘ§»τ÷±œΏy=2x”κΥΪ«ζœΏCΫΜ”ΎPΓΔQΝΫΒψΘ§«“ΥΡ±Ώ–ΈPF1QF2 «ΨΊ–ΈΘ§‘ρΥΪ«ζœΏΒΡάκ–Ρ¬ ΈΣΘ®ΓΓΓΓΘ©
“―÷ΣF1Θ§F2 «ΥΪ«ζœΏCΘΚ$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1Θ®aΘΨ0$Θ§bΘΨ0Θ©ΒΡΉσΓΔ”“ΫΙΒψΘ§»τ÷±œΏy=2x”κΥΪ«ζœΏCΫΜ”ΎPΓΔQΝΫΒψΘ§«“ΥΡ±Ώ–ΈPF1QF2 «ΨΊ–ΈΘ§‘ρΥΪ«ζœΏΒΡάκ–Ρ¬ ΈΣΘ®ΓΓΓΓΘ©| AΘ° | $5-2\sqrt{5}$ | BΘ° | $5+2\sqrt{5}$ | CΘ° | $\sqrt{5+2\sqrt{5}}$ | DΘ° | $\sqrt{5-2\sqrt{5}}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 10 | BΘ° | -10 | CΘ° | 0 | DΘ° | -5 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ≥δΖ÷≤Μ±Ί“ΣΧθΦΰ | BΘ° | ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰ | ||
| CΘ° | ≥δΖ÷±Ί“ΣΧθΦΰ | DΘ° | Φ»≤Μ≥δΖ÷“≤≤Μ±Ί“ΣΧθΦΰ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com