
分析 求得两圆的圆心和半径,设双曲线x2-$\frac{{y}^{2}}{8}$=1的左右焦点为F1(-3,0),F2(3,0),连接PF1,PF2,F1A,F2B,运用勾股定理和双曲线的定义,结合三点共线时,距离之和取得最小值,计算即可得到所求值.
解答 9 解:圆C1:(x+3)2+y2=4的圆心为(-3,0),半径为r1=2;
解:圆C1:(x+3)2+y2=4的圆心为(-3,0),半径为r1=2;
圆C2:(x-3)2+y2=1的圆心为(3,0),半径为r2=1,
设双曲线x2-$\frac{{y}^{2}}{8}$=1的左右焦点为F1(-3,0),F2(3,0),
连接PF1,PF2,F1A,F2B,可得
|PA|2-|PB|2=(|PF1|2-r12)-(|PF2|2-r22)
=(|PF1|2-4)-(|PF2|2-1)
=|PF1|2-|PF2|2-3=(|PF1|-|PF2|)(|PF1|+|PF2|)-3
=2a(|PF1|+|PF2|-3=2(|PF1|+|PF2|)-3≥2•2c-3=2•6-3=9.
当且仅当P为右顶点时,取得等号,
即最小值9.
故答案为:9
点评 本题考查最值的求法,注意运用双曲线的定义和圆的方程,考查三点共线的性质,以及运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<3} | B. | {x|-1<x<2} | C. | {x|-3<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
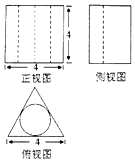
| A. | $16\sqrt{3}-\frac{16π}{3}$ | B. | $\frac{{16\sqrt{3}-16π}}{3}$ | C. | $8\sqrt{3}-\frac{8π}{3}$ | D. | $\frac{{8\sqrt{3}-8π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
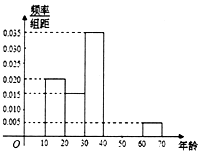 2017年由央视举办的一档文化益智节目《中国诗词大会》深受观众喜爱,某记者调查了部分年龄在[10,70]的观众,得到如下频率分布直方图.若第四、五、六组的人数依次成等差数列,且第六组有4人.
2017年由央视举办的一档文化益智节目《中国诗词大会》深受观众喜爱,某记者调查了部分年龄在[10,70]的观众,得到如下频率分布直方图.若第四、五、六组的人数依次成等差数列,且第六组有4人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}x±2y=0$ | B. | $2x±\sqrt{10}y=0$ | C. | $\sqrt{6}x±2y=0$ | D. | $2x±\sqrt{6}y=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
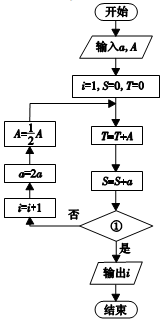 我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:| A. | T>2S? | B. | S>2T? | C. | S<2T? | D. | T<2S? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com