
分析 (1)利用相互独立事件的概率计算公式即可得出.
(2)利用相互独立事件与互斥事件的概率计算公式及其分布列与数学期望计算公式即可得出
解答 解:(1)M与B1,B2,B3进行对抗赛获胜的事件分别为A,B,C,M至少获胜两场的事件为D,
则P(A)=$\frac{4}{5}$,P(B)=$\frac{2}{3}$,P(C)=$\frac{1}{2}$由于事件A,B,C相互独立,
所以P(D)=P(ABC)+P$(\overline{A}BC)$+$P(A\overline{B}C)$+P($AB\overline{C}$)=$\frac{4}{5}$×$\frac{2}{3}$×$\frac{1}{2}$+(1-$\frac{4}{5}$)×$\frac{2}{3}$×$\frac{1}{2}$+$\frac{4}{5}$×(1-$\frac{2}{3}$)×$\frac{1}{2}$+$\frac{4}{5}$×$\frac{2}{3}$×(1-$\frac{1}{2}$)=$\frac{11}{15}$,
由于$\frac{11}{15}=\frac{22}{30}$$>\frac{21}{30}$=$\frac{7}{10}$,所以M会入选下一轮.
(2)M获胜场数X的可能取值为0,1,2,3,则P(X=0)=(1-$\frac{4}{5}$)×(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)=$\frac{1}{30}$,
P(X=1)=(1-$\frac{4}{5}$)×(1-$\frac{2}{3}$)×$\frac{1}{2}$+(1-$\frac{4}{5}$)×$\frac{2}{3}$×(1-$\frac{1}{2}$)+$\frac{4}{5}$×(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)=$\frac{7}{30}$,
P(X=2)=(1-$\frac{4}{5}$)×$\frac{2}{3}$×$\frac{1}{2}$+$\frac{4}{5}$×(1-$\frac{2}{3}$)×$\frac{1}{2}$+$\frac{4}{5}$×$\frac{2}{3}$×(1-$\frac{1}{2}$)=$\frac{14}{30}$,
P(X=3)=$\frac{4}{5}$×$\frac{2}{3}$×$\frac{1}{2}$=$\frac{8}{30}$.
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{30}$ | $\frac{7}{30}$ | $\frac{14}{30}$ | $\frac{8}{30}$ |
点评 本题考查了相互独立与互斥事件的概率计算公式、随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
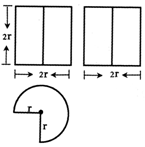
| A. | 18π+16 | B. | 20π+16 | C. | 22π+16 | D. | 24π+16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {-2,-1} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com