
| A. | 0 | B. | 504 | C. | 1008 | D. | 2016 |
分析 使用二项式定理化简得f(x)═(x-$\frac{1}{2}$)3+$\frac{1}{4}$.根据$\frac{k}{2017}-\frac{1}{2}$与$\frac{2017-k}{2017}-\frac{1}{2}$互为相反数便可得出答案.
解答 解:f(x)=x3-$\frac{3}{2}{x^2}+\frac{3}{4}x+\frac{1}{8}$=x3-$\frac{3}{2}$x2+$\frac{3}{4}$x-$\frac{1}{8}$+$\frac{1}{4}$=(x-$\frac{1}{2}$)3+$\frac{1}{4}$.
∵$\frac{k}{2017}-\frac{1}{2}$+$\frac{2017-k}{2017}-\frac{1}{2}$=0,k=1,2,…2016.
∴($\frac{k}{2017}$-$\frac{1}{2}$)3+($\frac{2017-k}{2017}-\frac{1}{2}$)3=0,k=1,2,…2016.
∴$\sum_{k=1}^{2016}{f({\frac{k}{2017}})}$=$\frac{1}{4}×2016$=504.
故选:B.
点评 本题考查了二项式定理的应用,属于中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | [-2,1) | C. | {0,1,2} | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
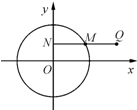 如图,已知点M在圆O:x2+y2=4上运动,MN⊥y轴(垂足为N),点Q在NM的延长线上,且|QN|=2|MN|.
如图,已知点M在圆O:x2+y2=4上运动,MN⊥y轴(垂足为N),点Q在NM的延长线上,且|QN|=2|MN|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com