
分析 (Ⅰ)把已知数列递推式变形,求得${S}_{n}={n}^{2}+2n$,得到数列首项,再由an=Sn-Sn-1(n≥2)求{an}的通项公式an;
(Ⅱ)把(Ⅰ)中求得的通项公式代入bn=$\frac{{a}_{n}-5}{{2}^{n}}$,得到b2n,再由错位相减法求得b2+b4+…+b2n.
解答 解:(Ⅰ)由Sn2-(n2+2n-1)Sn-(n2+2n)=0,得[${S}_{n}-({n}^{2}+2n)$](Sn+1)=0,
由an>0,可知Sn>0,故${S}_{n}={n}^{2}+2n$.
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=({n}^{2}+2n)-[(n-1)^{2}+2(n-1)]$=2n+1;
当n=1时,a1=S1=3,符合上式,
则数列{an}的通项公式为an=2n+1.
(Ⅱ) 解:依题意,bn=$\frac{{a}_{n}-5}{{2}^{n}}$=$\frac{2n-4}{{2}^{n}}=\frac{n-2}{{2}^{n-1}}$,
则${b}_{2n}=\frac{2n-2}{{2}^{2n-1}}=(n-1)•(\frac{1}{4})^{n-1}$,
设Tn=b2+b4+…+b2n,
故${T}_{n}=0+\frac{1}{4}+\frac{2}{{4}^{2}}+\frac{3}{{4}^{3}}+…+\frac{n-1}{{4}^{n-1}}$,
而$4{T}_{n}=1+\frac{2}{4}+\frac{3}{{4}^{2}}+…+\frac{n-1}{{4}^{n-2}}$.
两式相减,得$3{T}_{n}=1+\frac{1}{4}+\frac{1}{{4}^{2}}+…+\frac{1}{{4}^{n-2}}-\frac{n-1}{{4}^{n-1}}$=$\frac{1-(\frac{1}{4})^{n-1}}{1-\frac{1}{4}}-\frac{n-1}{{4}^{n-1}}=\frac{1}{3}(4-\frac{3n+1}{{4}^{n-1}})$,
故${T}_{n}=\frac{1}{9}(4-\frac{3n+1}{{4}^{n-1}})$.
点评 本题考查数列递推式,考查了由数列的前n项和求数列的通项公式,训练了错位相减法求数列的通项公式,是中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
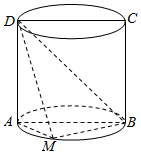 如图所示,已知四边形ABCD是圆柱的轴截面,M是下底面圆周上不与点A,B重合的点.
如图所示,已知四边形ABCD是圆柱的轴截面,M是下底面圆周上不与点A,B重合的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com