
分析 (Ⅰ)设等比数列{an}的公比为q.当q=1时,显然S3+S6≠2S9,与已知S3,S9,S6成等差数列矛盾,可得q≠1.由S3+S6=2S9,利用求和公式化为:1+q3=2q6,即可证明a2,a8,a5成等差数列.
(Ⅱ)由(Ⅰ)1+q3=2q6,解得q3=-$\frac{1}{2}$.可得${a}_{n}^{3}$=$({a}_{1}{q}^{n-1})^{3}$=${a}_{2}^{3}•{q}^{3(n-2)}$=$(-\frac{1}{2})^{n-2}$.b1=a2=1,b3=a5=-$\frac{1}{2}$,可得bn=-$\frac{3}{4}n$+$\frac{7}{4}$,${a}_{n}^{3}{b}_{n}$=$(-\frac{3}{4}n+\frac{7}{4})$$(-\frac{1}{2})^{n-2}$,再利用“错位相减法”与等比数列的求和公式即可得出.
解答 (Ⅰ)证明:设等比数列{an}的公比为q.
当q=1时,显然S3+S6≠2S9,与已知S3,S9,S6成等差数列矛盾,
∴q≠1.由S3+S6=2S9,可得$\frac{{a}_{1}(1-{q}^{3})}{1-q}$+$\frac{{a}_{1}(1-{q}^{6})}{1-q}$=2$•\frac{{a}_{1}(1-{q}^{9})}{1-q}$,
化为:1+q3=2q6,∴a2+a5=${a}_{2}(1+{q}^{3})$=${a}_{2}•2{q}^{6}$=2a8.
∴a2,a8,a5成等差数列.
(Ⅱ)解:由(Ⅰ)1+q3=2q6,解得q3=1(舍去),q3=-$\frac{1}{2}$.
∴${a}_{n}^{3}$=$({a}_{1}{q}^{n-1})^{3}$=${a}_{2}^{3}•{q}^{3(n-2)}$=$(-\frac{1}{2})^{n-2}$.
b1=a2=1,b3=a5=-$\frac{1}{2}$,
数列{bn}的公差d=$\frac{1}{2}$(b3-b1)=-$\frac{3}{4}$.
∴bn=-$\frac{3}{4}n$+$\frac{7}{4}$,
故${a}_{n}^{3}{b}_{n}$=$(-\frac{3}{4}n+\frac{7}{4})$$(-\frac{1}{2})^{n-2}$,
Tn=$1×(-\frac{1}{2})^{-1}$+$\frac{1}{4}(-\frac{1}{2})^{0}+(-\frac{2}{4})(-\frac{1}{2})^{1}$+…+$(-\frac{3}{4}n+\frac{7}{4})$$(-\frac{1}{2})^{n-2}$,①
$-\frac{1}{2}{T}_{n}$=$1×(-\frac{1}{2})^{0}+\frac{1}{4}$$(-\frac{1}{2})^{1}$+…+$(-\frac{3}{4}n+\frac{10}{4})$$(-\frac{1}{2})^{n-2}$+$(-\frac{3}{4}n+\frac{7}{4})$$(-\frac{1}{2})^{n-1}$ ②
①-②得:$\frac{3}{2}{T}_{n}$=-2+$(-\frac{3}{4})$$[(-\frac{1}{2})^{0}+(-\frac{1}{2})^{1}+…+(-\frac{1}{2})^{n-2}]$-$(-\frac{3}{4}n+\frac{7}{4})$$(-\frac{1}{2})^{n-1}$=-2-$\frac{1}{2}[1-(-\frac{1}{2})^{n-1}]$-$(-\frac{3}{4}n+\frac{7}{4})$$(-\frac{1}{2})^{n-1}$=$-\frac{5}{2}$+$(\frac{3}{4}n-\frac{5}{4})$$(-\frac{1}{2})^{n-1}$,
解得Tn=-$\frac{5}{3}$+$\frac{5-3n}{3}(-\frac{1}{2})^{n}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、“错位相减法”方法,考查了推理能力与计算能力,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{6}$-5 | B. | -5 | C. | 2$\sqrt{6}$+5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{π}{4}+kπ,\frac{π}{4}+kπ}](k∈Z)$ | B. | $[{\frac{π}{4}+kπ,\frac{3π}{4}+kπ}](k∈Z)$ | ||
| C. | $[{\frac{π}{12}+kπ,\frac{7π}{12}+kπ}](k∈Z)$ | D. | $[{-\frac{5π}{12}+kπ,\frac{π}{12}+kπ}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
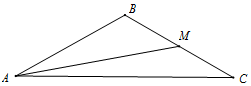 如图,在△ABC中,M是边BC的中点,tan∠BAM=$\frac{\sqrt{3}}{5}$,cos∠AMC=-$\frac{2\sqrt{7}}{7}$
如图,在△ABC中,M是边BC的中点,tan∠BAM=$\frac{\sqrt{3}}{5}$,cos∠AMC=-$\frac{2\sqrt{7}}{7}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{5{e}^{2}}$,$\frac{1}{3e}$) | B. | [$\frac{1}{3e}$,$\frac{\sqrt{e}}{4e}$) | C. | [$\frac{1}{3e}$,e] | D. | [$\frac{\sqrt{e}}{4e}$,e] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com