
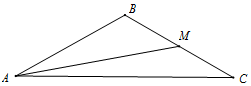
 如图,在△ABC中,M是边BC的中点,tan∠BAM=$\frac{\sqrt{3}}{5}$,cos∠AMC=-$\frac{2\sqrt{7}}{7}$
如图,在△ABC中,M是边BC的中点,tan∠BAM=$\frac{\sqrt{3}}{5}$,cos∠AMC=-$\frac{2\sqrt{7}}{7}$分析 (Ⅰ)由邻补角定义及诱导公式得到cos∠AMC=-cos∠AMB,求出cos∠AMB的值,利用同角三角函数间的基本关系求出tan∠AMB的值,再利用诱导公式求出tanB的值,即可确定出B的大小;
(Ⅱ)由三角形内角和定理及等角对等边得到AB=BC,设BM=x,则AB=BC=2x,利用余弦定理列出方程,求出方程的解得到x的值,确定出AB与BC的值,再利用三角形面积公式求出三角形ABC面积即可.
解答 解:(Ⅰ)由题意可知∠AMB+∠AMC=π,
又cos∠AMC=-$\frac{2\sqrt{7}}{7}$,
∴cos∠AMB=$\frac{2\sqrt{7}}{7}$,sin∠AMB=$\frac{\sqrt{21}}{7}$,tan∠AMB=$\frac{\sqrt{3}}{2}$,
∴tanB=-tan(∠BAM+∠BMA)=-$\frac{tan∠BAM+tan∠BMA}{1-tan∠BAM•tan∠BMA}$=-$\frac{\frac{\sqrt{3}}{5}+\frac{\sqrt{3}}{2}}{1-\frac{\sqrt{3}}{5}×\frac{\sqrt{3}}{2}}$=-$\sqrt{3}$,
又B∈(0,π),
∴B=$\frac{2π}{3}$;
(Ⅱ)由(Ⅰ)知∠B=$\frac{2π}{3}$,且∠BAC=$\frac{π}{6}$,
∴∠C=$\frac{π}{6}$,即∠BAC=∠C,
∴AB=BC,
设BM=x,则AB=2x,
在△AMB中,由余弦定理得AM2=AB2+BM2-2AB•BM•cosB,即7=4x2+x2+2x2,
解得:x=1(负值舍去),
∴AB=BC=2,
则S△ABC=$\frac{1}{2}$•4•sin$\frac{2π}{3}$=$\sqrt{3}$.
点评 此题考查了余弦定理,三角形面积公式,诱导公式,以及同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{176}{3}$ | B. | $\frac{160}{3}$ | C. | $\frac{128}{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}$ | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com