练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}{x=-2+2cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρsin（θ+$\frac{π}{4}$）=2$\sqrt{2}$
    （Ⅰ）直接写出C1的普通方程和极坐标方程，直接写出C2的普通方程；
    （Ⅱ）点A在C1上，点B在C2上，求|AB|的最小值．

    分析 （Ⅰ）把圆C1的参数方程变形，两式平方作和可得普通方程，进一步求得极坐标方程，展开两角和的正弦，结合x=ρcosθ，y=ρsinθ可得C2的普通方程；
    （Ⅱ）由点到直线的距离公式求出圆心到直线的距离，可得直线和圆相离，由点到直线的距离减去圆的半径求得|AB|的最小值．

    解答 解：（Ⅰ）由$\left\{\begin{array}{l}{x=-2+2cosθ}\\{y=2sinθ}\end{array}\right.$，得$\left\{\begin{array}{l}{x+2=2cosθ}\\{y=2sinθ}\end{array}\right.$，两式平方作和得：（x+2）2+y2=4，
    C1的极坐标方程为ρ=-4cosθ，
    由ρsin（θ+$\frac{π}{4}$）=2$\sqrt{2}$，得$ρsinθcos\frac{π}{4}+ρcosθsin\frac{π}{4}=2\sqrt{2}$，
    即$\frac{\sqrt{2}}{2}ρsinθ+\frac{\sqrt{2}}{2}ρcosθ=2\sqrt{2}$，
    得x+y-4=0．
    （Ⅱ）C1是以点（-2，0）为圆心，半径为2的圆，C2是直线．
    圆心到直线C2的距离为$\frac{|-2+0-4|}{\sqrt{2}}=3\sqrt{2}$＞2，直线和圆相离．
    ∴|AB|的最小值为$3\sqrt{2}-2$．

    点评 本题考查解得曲线的极坐标方程，考查参数方程和普通方程的互化，训练了直线与圆位置关系的应用，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．函数$f（x）=cos（ωx+\frac{π}{6}）（ω＞0）$的最小正周期是π，则其图象向右平移$\frac{π}{3}$个单位后的单调递减区间是（　　）
    A．$[{-\frac{π}{4}+kπ，\frac{π}{4}+kπ}]（k∈Z）$B．$[{\frac{π}{4}+kπ，\frac{3π}{4}+kπ}]（k∈Z）$
    C．$[{\frac{π}{12}+kπ，\frac{7π}{12}+kπ}]（k∈Z）$D．$[{-\frac{5π}{12}+kπ，\frac{π}{12}+kπ}]（k∈Z）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

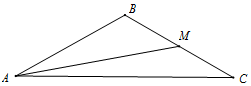    3．如图，在△ABC中，M是边BC的中点，tan∠BAM=$\frac{\sqrt{3}}{5}$，cos∠AMC=-$\frac{2\sqrt{7}}{7}$
    （Ⅰ）求角B的大小；
    （Ⅱ）若角∠BAC=$\frac{π}{6}$，BC边上的中线AM的长为$\sqrt{7}$，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设当x=α时，函数f（x）=3sinx+cosx取得最大值，则tan2α=$-\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒．若一名行人 来到该路口遇到红灯，则至少需要等待15秒才出现绿灯的概率为$\frac{5}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知点M（2$\sqrt{2}$，$\frac{2\sqrt{3}}{3}$）在椭圆G：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，且点M到两焦点距离之和为4$\sqrt{3}$．
    （1）求椭圆G的方程；
    （2）若斜率为1的直线l与椭圆G交于A，B两点，以AB为底作等腰三角形，顶点为P（-3，2），求△PAB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若关于x的不等式xex-2ax+a＜0的非空解集中无整数解，则实数a的取值范围是（　　）
    A．[$\frac{2}{5{e}^{2}}$，$\frac{1}{3e}$）B．[$\frac{1}{3e}$，$\frac{\sqrt{e}}{4e}$）C．[$\frac{1}{3e}$，e]D．[$\frac{\sqrt{e}}{4e}$，e]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=e2，g（x）=x2+ax-2a2+3a，（a∈R），记函数h（x）=g（x）•f（x）．
    （1）讨论函数h（x）的单调性；
    （2）试比较ef（x-2）与x的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设函数f'（x）是函数f（x）（x∈R）的导函数，f（0）=1，且$f（x）=\frac{1}{3}f'（x）-1$，则4f（x）＞f'（x）的解集为（　　）
    A．$（\frac{ln4}{3}，+∞）$B．$（\frac{ln2}{3}，+∞）$C．$（\frac{{\sqrt{3}}}{2}，+∞）$D．$（\frac{{\sqrt{e}}}{3}，+∞）$

    查看答案和解析>>

    同步练习册答案