练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．从某班的20名学生（其中男学生8名）中选出5名，参加学校举行的跳绳团体赛．
    （1）若甲学生与乙学生必须参加，则有多少种不同的选法？
    （2）若甲、乙两名学生至少有1人参加，则有多少种不同的选法？
    （3）若至少有1名女学生和1名男学生，则有多少种不同的选法？

    分析 （1）甲学生与乙学生必须参加，再从剩下的18人选选3人，问题得以解决，
    （2）甲、乙两名学生至少有1人参加，先求出没有条件的种数，再排除没有甲乙的种数，问题得以解决，
    （3）至少有1名女学生和1名男学生，男生8名，女生12名，先求出没有限制条件的，再排除全是男生和全是女生的，问题得以解决．

    解答 解：（1）甲学生与乙学生必须参加，再从剩下的18人选选3人，故有C183=816种，
    （2）甲、乙两名学生至少有1人参加，先求出没有条件的种数，再排除没有甲乙的种数，故有C205-C185=6936种，
    （3）至少有1名女学生和1名男学生，男生8名，女生12名，先求出没有限制条件的，再排除全是男生和全是女生的，
    故有C205-C125-C85=14656种．

    点评 本题考查排列、组合的应用，正确利用间接法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．△ABC的三内角A，B，C的对边分别是a，b，c，则“a2+b2＜c2”是“△ABC为钝角三角形”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=ex-e-x（x∈R，e=2.71828…）
    （Ⅰ）求证：函数f（x）为奇函数；
    （Ⅱ）t为实数，且f（x-t）+f（x2-t2）≥0对一切实数x都成立，求t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．大楼的顶上有一座电视塔，高20米，在地面某处测得塔顶的仰角为45°，塔底的仰角为30°，求此大楼的高度（保留两位小数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设z是纯虚数，若$\frac{1-i}{z+2}$是实数，则z=（　　）
    A．-2iB．-iC．iD．2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．某小区有排成一排的8个车位，现有5辆不同型号的轿车需要停放，则这5辆轿车停入车位后，剩余3个车位连在一起的概率为$\frac{3}{28}$（结果用最简分数表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

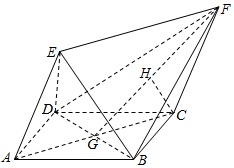    1．四边形ABCD为菱形，ACFE为平行四边形，且平面ACFE⊥平面ABCD，设BD与AC相交于点G，H为FG的中点，AB=BD=2，AE=$\sqrt{3}$，CH=$\frac{{\sqrt{3}}}{2}$．
    （Ⅰ）求证：CH⊥平面BDF
    （Ⅱ）求三棱锥B-DEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．数列{an}的前n项和为Sn，a1=1，an+a2n=n，a2n+1=an+1，则S49=325．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．“六一”儿童节这天，糖果店的售货员忙极了，请你设计一个程序，帮助售货员算账，已知水果糖每千克10元，奶糖每千克15元，巧克力糖每千克25元，那么依次购买这三种糖果a，b，c千克，应收取多少元钱？写出一个算法，画出程序框图．

    查看答案和解析>>

    同步练习册答案