
【题目】函数![]() 的值域为_________________.
的值域为_________________.
【答案】[-1,1)
【解析】
由题可得![]() ,由
,由![]() 易得0<
易得0<![]() ≤2,
≤2,
故y∈[-1,1),所以函数![]() 的值域为[-1,1) .
的值域为[-1,1) .
【解题必备】(1)在高考中考查函数的定义域时多以客观题形式呈现,难度不大.求函数定义域的三种常考类型及求解策略:①已知函数的解析式:构建使解析式有意义的不等式(组)求解;②对于抽象函数:若已知函数f(x)的定义域为[a,b],则复合函数f(g(x))的定义域由a≤g(x)≤b求出,若已知函数f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在x∈[a,b]时的值域;③对于实际问题:既要使构建的函数解析式有意义,又要考虑实际问题的要求.
(2)求函数定义域的注意点:①不要对解析式进行化简变形,以免定义域变化;②当一个函数由有限个基本初等函数的和、差、积、商的形式构成时,定义域一般是各个基本初等函数定义域的交集;③定义域是一个集合,要用集合或区间表示,若用区间表示,不能用“或”连接,而应该用并集符号“∪”连接.
(3)求函数值域的基本方法:①观察法,通过对函数解析式的简单变形,利用熟知的基本函数的值域,或利用函数图象的“最高点”和“最低点”,观察求得函数的值域;②利用常见函数的值域,一次函数的值域为![]() ,反比例函数的值域为
,反比例函数的值域为![]() ,指数函数的值域为
,指数函数的值域为![]() ,对数函数的值域为
,对数函数的值域为![]() ,正、余弦函数的值域为
,正、余弦函数的值域为![]() ,正切函数的值域为
,正切函数的值域为![]() ;③分离常数法,将形如
;③分离常数法,将形如![]() (a≠0)的函数分离常数,结合x的取值范围确定函数的值域;④换元法,对某些无理函数或其他函数,通过适当的换元,把它们化为我们熟悉的函数,再用有关方法求值域;⑤配方法,对二次函数型的解析式可以先进行配方,在充分注意到自变量取值范围的情况下,利用求二次函数的值域的方法求函数的值域;⑥数形结合法,作出函数图象,找出自变量对应的范围或分析条件的几何意义,在图上找出值域;⑦单调性法(也可结合导数),函数单调性的变化是求最值和值域的依据,根据函数的单调区间判断其单调性,进而求函数的最值和值域;⑧基本不等式法,利用基本不等式
(a≠0)的函数分离常数,结合x的取值范围确定函数的值域;④换元法,对某些无理函数或其他函数,通过适当的换元,把它们化为我们熟悉的函数,再用有关方法求值域;⑤配方法,对二次函数型的解析式可以先进行配方,在充分注意到自变量取值范围的情况下,利用求二次函数的值域的方法求函数的值域;⑥数形结合法,作出函数图象,找出自变量对应的范围或分析条件的几何意义,在图上找出值域;⑦单调性法(也可结合导数),函数单调性的变化是求最值和值域的依据,根据函数的单调区间判断其单调性,进而求函数的最值和值域;⑧基本不等式法,利用基本不等式![]() (a>0,b>0)求最值,注意应用基本不等式的条件是“一正二定三相等”;⑨判别式法,将函数转化为二次方程,利用Δ≥0,由此确定函数的值域,利用判别式求函数值的范围,常用于一些“分式”函数、“无理”函数等,使用此法要特别注意自变量的取值范围;⑩有界性法,充分利用三角函数或一些代数表达式的有界性,求出值域.
(a>0,b>0)求最值,注意应用基本不等式的条件是“一正二定三相等”;⑨判别式法,将函数转化为二次方程,利用Δ≥0,由此确定函数的值域,利用判别式求函数值的范围,常用于一些“分式”函数、“无理”函数等,使用此法要特别注意自变量的取值范围;⑩有界性法,充分利用三角函数或一些代数表达式的有界性,求出值域.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,x轴正半轴为极轴建立极坐标系中,直线
为极点,x轴正半轴为极轴建立极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求出线![]() 的极坐标方程及直线
的极坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 为曲线
为曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离最大值.
的距离最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知四棱锥![]() 的侧棱长与底面边长都相等,四边形
的侧棱长与底面边长都相等,四边形![]() 为正方形,点
为正方形,点![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

(2)如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某自然资源探险组织试图穿越某峡谷,但峡谷内被某致命昆虫所侵扰,为了穿越这个峡谷,该探险组织进行了详细的调研,若每平方米的昆虫数量记为昆虫密度![]() ,调研发现,在这个峡谷中,昆虫密度
,调研发现,在这个峡谷中,昆虫密度![]() 是时间
是时间![]() (单位:小时)的一个连续不间断的函数其函数表达式为
(单位:小时)的一个连续不间断的函数其函数表达式为
 ,
,
其中时间![]() 是午夜零点后的小时数,
是午夜零点后的小时数,![]() 为常数.
为常数.
(1)求![]() 的值;
的值;
(2)求出昆虫密度的最小值和出现最小值的时间![]() ;
;
(3)若昆虫密度不超过1250只/平方米,则昆虫的侵扰是非致命性的,那么在一天24小时内哪些时间段,峡谷内昆虫出现非致命性的侵扰.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“整治散落污染企业”等.下表是该市2016年11月份和2017年11月份的空气质量指数(![]() )(
)(![]() 指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
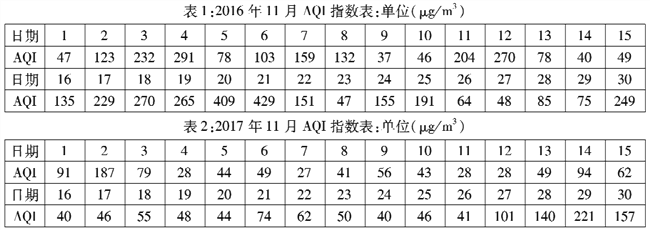
(1)将2017年11月的空气质量指数![]() 数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个
数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个![]() 数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
(2)从(1)中抽出的6个样本数据中随机抽取2个,求这2个![]() 数据之差的绝对值小于30的概率;
数据之差的绝对值小于30的概率;
(3)根据《环境空气质量指数(![]() )技术规定(试行)》规定:当空气质量指数为
)技术规定(试行)》规定:当空气质量指数为![]() (含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
(含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() ,
,![]() 为斜边
为斜边![]() 的中点,且
的中点,且![]() 平行于
平行于![]() 轴.
轴.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .以
.以![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 、
、![]() ,记此圆的圆心为
,记此圆的圆心为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 点处的切线方程;
点处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围;
的取值范围;
(3)求证:对于任意大于![]() 的正整数
的正整数![]() ,都有
,都有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com