
分析 (1)利用向量模的坐标公式求出|$\overrightarrow{{a}_{n}}$|的模,得到|$\overrightarrow{{a}_{n}}$|与|$\overrightarrow{{a}_{n-1}}$|的关系,利用等比数列的定义能证明数列$\left\{{|{\overrightarrow{a_n}}|}\right\}$是等比数列.
(2)利用向量的坐标形式的数量积公式求出$\overrightarrow{{a}_{n-1}}$,$\overrightarrow{{a}_{n}}$的数量积,利用向量的模、夹角形式的数量积公式求出夹角的余弦,从而得到bn=$\frac{n^2}{π}{θ_n}$=$\frac{{n}^{2}}{4}$,由此能求出结果.
解答 证明:(1)∵向量列$\left\{{\overrightarrow{a{\;}_n}}\right\}$满足:$\overrightarrow{a_1}$=(1,1),
$\overrightarrow{a_n}$=(xn,yn)=$\frac{1}{2}$(xn-1-yn-1,xn-1+yn-1),
∴|$\overrightarrow{{a}_{n}}$|=$\frac{1}{2}\sqrt{({x}_{n-1}-{y}_{n-1})^{2}-({x}_{n-1}+{y}_{n-1})^{2}}$
=$\frac{\sqrt{2}}{2}$$\sqrt{{{x}_{n-1}}^{2}+{{y}_{n-1}}^{2}}$
=$\frac{\sqrt{2}}{2}$|$\overrightarrow{{a}_{n-1}}$|,
∴数列$\left\{{|{\overrightarrow{a_n}}|}\right\}$是等比数列.
解:(2)∵θn表示向量$\overrightarrow{a_n}$与$\overrightarrow{{a_{n-1}}}$间的夹角,
∴cosQn=$\frac{\overrightarrow{{a}_{n-1}}•\overrightarrow{{a}_{n}}}{|\overrightarrow{{a}_{n-1}}|•|\overrightarrow{{a}_{n}}|}$=$\frac{({x}_{n-1},{y}_{n-1})•\frac{1}{2}({x}_{n-1}-{y}_{n-1},{x}_{n-1}+{y}_{n-1})}{\frac{\sqrt{2}}{2}|\overrightarrow{{a}_{n-1}}{|}^{2}}$
=$\frac{\frac{1}{2}({{x}_{n-1}}^{2}+{{y}_{n-1}}^{2})}{\frac{\sqrt{2}}{2}({{x}_{n-1}}^{2}+{{y}_{n-1}}^{2})}$=$\frac{\sqrt{2}}{2}$,
∴Qn=$\frac{π}{4}$,bn=$\frac{n^2}{π}{θ_n}$=$\frac{{n}^{2}}{4}$,
∴$\sqrt{\frac{1}{{{b_{n+1}}}}}$+$\sqrt{\frac{1}{{{b_{n+2}}}}}$+…+$\sqrt{\frac{1}{{{b_{2n}}}}}$=$\frac{2}{n+1}+\frac{2}{n+2}+…+\frac{2}{2n}$,
记f(n)=$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,
则f(n+1)-f(n)=$\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$=$\frac{1}{2n+1}-\frac{1}{2n+2}$=$\frac{1}{(2n+1)(2n+2)}$>0,
∴f(n)随n单调增加,
∴f(n)>m对于一切大于1的自然数n都成立等价于m<f(2)=$\frac{1}{3}+\frac{1}{4}$=$\frac{7}{12}$,
∵对于任意正整数n,不等式$\sqrt{\frac{1}{{{b_{n+1}}}}}$+$\sqrt{\frac{1}{{{b_{n+2}}}}}$+…+$\sqrt{\frac{1}{{{b_{2n}}}}}$=$\frac{2}{n+1}+\frac{2}{n+2}+…+\frac{2}{2n}$>a(a+2)恒成立,
∴a(a+2)<2f(2)=$\frac{7}{6}$,
解得-1-$\frac{\sqrt{78}}{6}$<a<-1+$\frac{\sqrt{78}}{6}$,
∴实数a的范围是(-1-$\frac{\sqrt{78}}{6}$,-1+$\frac{\sqrt{78}}{6}$).
点评 解决向量的夹角问题一般利用向量的数量积公式求出夹角余弦,再利用夹角范围求出夹角;求数列的前n项和问题,应该先求出数列的通项,据通项的特点选择求和方法.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{\sqrt{3}}{2}$]∪[$\frac{\sqrt{3}}{2}$,+∞) | B. | [-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$] | C. | (-∞,-$\frac{\sqrt{3}}{2}$]∪($\frac{\sqrt{3}}{2}$,+∞) | D. | (-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
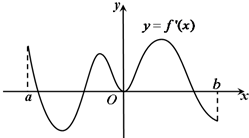 函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )
函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com