
分析 构造函数g(x)=(1+x)ln2(x+1)-x2,(x>-1).求出导数,再令h(x)=ln2(x+1)+2ln(x+1)-2x,求出导数,再令u(x)=ln(x+1)-x,x∈(0,1],求出导数,判断u(x)的单调性,可得g(x)的单调性,即有(1+x)ln2(x+1)-x2<0,求出f(x)的导数,求得f(x)在(0,1]递减,可得f(1)取得最小值.
解答 解:∵函数g(x)=(1+x)ln2(x+1)-x2,(x>-1).
∴g′(x)=ln2(x+1)+2ln(x+1)-2x.
令h(x)=ln2(x+1)+2ln(x+1)-2x,
则h′(x)=$\frac{2ln(x+1)-2x}{x+1}$.
设u(x)=ln(x+1)-x,x∈(0,1],
则u′(x)=$\frac{1}{x+1}$-1<0,
∴u(x)在(0,1]上单调递减,
∴u(x)<u(0)=0.
∴h′(x)=$\frac{2ln(x+1)-2x}{x+1}$<0,
∴h(x)在(0,1]上单调递减,
∴h(x)<h(0)=0,
∴g′(x)在(0,1]上单调递减,∴g′(x)<g′(0)=0,
∴g(x)在(0,1]上单调递减.
有g(1)≤g(x)<g(0)=0,即g(x)=(1+x)ln2(x+1)-x2<0,
则函数f(x)=$\frac{1}{ln(x+1)}$-$\frac{1}{x}$的导数为f′(x)=$\frac{1}{{x}^{2}}$-$\frac{1}{(x+1)l{n}^{2}(x+1)}$
=$\frac{(x+1)l{n}^{2}(x+1)-{x}^{2}}{{x}^{2}(x+1)l{n}^{2}(x+1)}$<0,
∴f(x)在(0,1]上单调递减,于是f(1)≤f(x)<f(0),
∴f(x)在(0,1]上的最小值为f(1)=$\frac{1}{ln2}$-1.
点评 本题考查导数的运用:求单调区间,熟练掌握利用导数研究函数的单调性,并运用单调性是解题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}-1$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.
如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-2,-1)∪(-1,0) | C. | (-∞,-2)∪(0,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均数为10,方差为2 | B. | 平均数为11,方差为3 | ||
| C. | 平均数为11,方差为2 | D. | 平均数为12,方差为4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
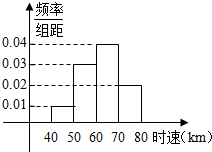
| A. | 60辆 | B. | 80辆 | C. | 70辆 | D. | 140辆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com