
| A. | 284 | B. | 285 | C. | 286 | D. | 287 |
分析 根据题意写出y的表达式,再设出$\overrightarrow{b}$=(cosθ,sinθ),计算出$\overrightarrow{{a}_{1}}$+$\overrightarrow{{a}_{2}}$+…+$\overrightarrow{{a}_{141}}$的结果,然后代入,运用正弦函数的值域,求出函数的最大值,进而得到答案.
解答 解:由向量$\overrightarrow{b}$为单位向量,可设$\overrightarrow{b}$=(cosθ,sinθ),
$\overrightarrow{{a}_{n}}$=(cos$\frac{nπ}{7}$,sin$\frac{nπ}{7}$),可得$\overrightarrow{{a}_{n}}$2=$\overrightarrow{b}$2=1,
则y=|$\overrightarrow{{a}_{1}}$+$\overrightarrow{b}$|2+|$\overrightarrow{{a}_{2}}$+$\overrightarrow{b}$|2+|$\overrightarrow{{a}_{3}}$+$\overrightarrow{b}$|2+…+|$\overrightarrow{{a}_{141}}$+$\overrightarrow{b}$|2
=($\overrightarrow{{a}_{1}}$2+$\overrightarrow{{a}_{2}}$2+…+$\overrightarrow{{a}_{141}}$2)+($\overrightarrow{b}$2+$\overrightarrow{b}$2+…+$\overrightarrow{b}$2)+2$\overrightarrow{b}$•($\overrightarrow{{a}_{1}}$+$\overrightarrow{{a}_{2}}$+…+$\overrightarrow{{a}_{141}}$)
=141+141+2(cosθ,sinθ)•(cos$\frac{π}{7}$+cos$\frac{2π}{7}$+…+cos$\frac{141π}{7}$,sin$\frac{π}{7}$+sin$\frac{2π}{7}$+…+sin$\frac{141π}{7}$),
由cos$\frac{π}{7}$+cos$\frac{2π}{7}$+…+cos$\frac{141π}{7}$=(cos$\frac{π}{7}$+cos$\frac{2π}{7}$+…+cos$\frac{14π}{7}$)+…+cos$\frac{141π}{7}$
=0×10+cos$\frac{π}{7}$=cos$\frac{π}{7}$,同理可得sin$\frac{π}{7}$+sin$\frac{2π}{7}$+…+sin$\frac{141π}{7}$=sin$\frac{π}{7}$,
即有y=282+2(cosθcos$\frac{π}{7}$+sinθsin$\frac{π}{7}$)=282+2cos(θ-$\frac{π}{7}$),
当cos(θ-$\frac{π}{7}$)=1,即θ=2kπ+$\frac{π}{7}$,k∈Z时,取得最大值284.
故选A.
点评 本题考查向量的数量积的坐标表示和性质,解决此类问题的关键是熟练掌握向量的有关基本运算以及有关三角恒等变换的运算.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
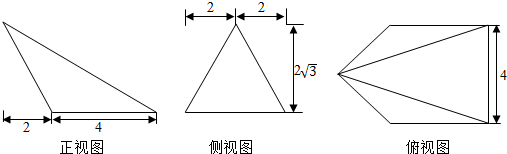
| A. | 48π | B. | 52π | C. | $\frac{172}{3}$π | D. | $\frac{196}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12>5 | B. | 若a为正无理数,则$\sqrt{a}$也是正无理数 | ||
| C. | 正弦函数是周期函数吗? | D. | π∈{1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com