
| A. | 为正 | B. | 为负 | C. | 为零 | D. | 为正或负 |
分析 把已知的等式两边平方,结合0<m<1及α的范围可得cosα<0,则则cosα-sinα=-$\sqrt{(cosα-sinα)^{2}}$,整理后可得cosα-sinα的值的符号.
解答 解:由sinα+cosα=m,得
(sinα+cosα)2=m2,即1+2sinα•cosα=m2,
∵0<m<1,
∴2sinα•cosα=m2-1<0,
由于α∈(0,π),sinα>0,从而cosα<0,
∴cosα-sinα<0,
则cosα-sinα=-$\sqrt{(cosα-sinα)^{2}}$=$-\sqrt{1-2sinαcosα}$
=$-\sqrt{1-({m}^{2}-1)}$=-$\sqrt{2-{m}^{2}}$,
则cosα-sinα的值为负.
故选:B.
点评 本题考查三角函数值符号的判定,由2sinα•cosα=m2-1<0,判断出cosα<0是解答该题的关键,是基础题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
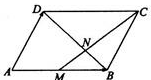 已知平行四边形ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,M为AB中点,N为BD靠近B的三等分点.
已知平行四边形ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,M为AB中点,N为BD靠近B的三等分点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com