
| A. | $\sqrt{0.52}$ | B. | $\sqrt{0.34}$ | C. | $\sqrt{0.69}$ | D. | $\sqrt{0.41}$ |
分析 如图所示,AB=2m,BD=0.3m,AD=2.3m,CD=xm,则tan∠BCD=$\frac{0.3}{x}$,tan∠ACD=$\frac{2.3}{x}$,利用tan∠ACB=tan(∠ACD-∠BCD)=$\frac{\frac{2.3}{x}-\frac{0.3}{x}}{1+\frac{2.3}{x}•\frac{0.3}{x}}$=$\frac{2}{x+\frac{0.69}{x}}$≤$\frac{1}{\sqrt{0.69}}$,即可得出结论.
解答 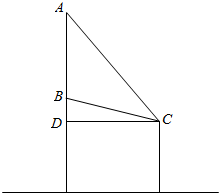 解:如图所示,AB=2m,BD=0.3m,AD=2.3m,CD=xm,则
解:如图所示,AB=2m,BD=0.3m,AD=2.3m,CD=xm,则
tan∠BCD=$\frac{0.3}{x}$,tan∠ACD=$\frac{2.3}{x}$,
tan∠ACB=tan(∠ACD-∠BCD)=$\frac{\frac{2.3}{x}-\frac{0.3}{x}}{1+\frac{2.3}{x}•\frac{0.3}{x}}$=$\frac{2}{x+\frac{0.69}{x}}$≤$\frac{1}{\sqrt{0.69}}$,
当且仅当x=$\frac{0.69}{x}$,即x=$\sqrt{0.69}$m,取等号,
此时观画者对此画所张的视角达到最大,
故选:C.
点评 本题考查利用数学知识解决实际问题,考查差角的正切公式,考查基本不等式的运用,正确转化是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
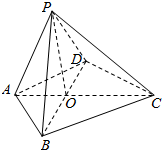 如图,四棱锥P-ABCD中,BC=CD,AB=AD=$\sqrt{2}$,AB⊥AD,O为BD的中点,PO⊥平面ABCD,平面PAB⊥平面PBC,设OC=a,PO=b.
如图,四棱锥P-ABCD中,BC=CD,AB=AD=$\sqrt{2}$,AB⊥AD,O为BD的中点,PO⊥平面ABCD,平面PAB⊥平面PBC,设OC=a,PO=b.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
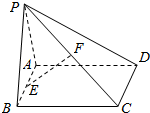 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{59}{117}$ | D. | $\frac{11}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com