
| A�� | n=1��֤����ȷ | B�� | ���ɼ��費��ȷ | ||
| C�� | ��n=k��n=k+1����������ȷ | D�� | ֤��������ȫ��ȷ |
���� ����ѧ���ɷ�֤������IJ����ǣ���һ������֤��n=n0ʱ����������ڶ������赱n=kʱ�����������ô��֤����n=k+1ʱ����Ҳ�������ؼ��ǵڶ�����Ҫ������Ϲ��ɼ���Ľ���
��� �⣺��n=1ʱ�����=$\sqrt{{1}^{2}+1}$=2���ұ�=1+1=2���ʵ�n=1ʱ������ʽ������
���赱n=k��k��N*��ʱ����ʽ��������$\sqrt{{k}^{2}+1}$��k+1����k2+1����k+1��2��
��n=k+1ʱ��$\sqrt{��k+1��^{2}+1}$=$\sqrt{{k}^{2}+2k+2}$��$\sqrt{��k+1��^{2}+2k+1}$=$\sqrt{��k+1��^{2}+2��k+1��+1-2}$=$\sqrt{��k+2��^{2}-2}$��$\sqrt{��k+2��^{2}}$=k+2=��k+1��+1��
�ʵ�n=k+1ʱ������ʽ������
��������������ʽ$\sqrt{{n}^{2}+1}$��n+1��n��N*����
�ɴ˿����жϴ�n=k��n=k+1����������ȷ�������ǣ�û�����ϼ��裬
��ѡ��C
���� ���⿼����ѧ���ɷ���˼�룬Ӧ����Ҫע��������Ϲ��ɼ���Ľ��ۣ�����ᵼ�´��������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 25 | B�� | -$\frac{25}{2}$ | C�� | $\frac{25}{2}$ | D�� | -25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
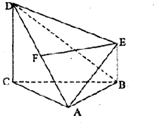 ��ͼ������A-BCDE�У�FΪAD���е㣬DC��ƽ��ABC��CD��BE��AB=AC=BC=CD=2BE��
��ͼ������A-BCDE�У�FΪAD���е㣬DC��ƽ��ABC��CD��BE��AB=AC=BC=CD=2BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com