
分析 确定区域的面积,即可求出事件“y<sin$\frac{π}{2}$x”发生的概率.
解答 解:在区间[-1,1]上随机地取两个数x、y,构成区域的面积为4;
事件“y<sin$\frac{π}{2}$x”发生,区域的面积为2${∫}_{0}^{1}$sin$\frac{π}{2}$xdx=2(-$\frac{2}{π}$)cos$\frac{π}{2}$x${|}_{0}^{1}$=$\frac{4}{π}$,
∴事件“y<sin$\frac{π}{2}$x”发生的概率为$\frac{1}{π}$.
故答案为$\frac{1}{π}$.
点评 本题考查概率的计算,考查学生的计算能力,确定区域的面积是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 6π | C. | 8π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n=1验证不正确 | B. | 归纳假设不正确 | ||
| C. | 从n=k到n=k+1的推理不正确 | D. | 证明过程完全正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
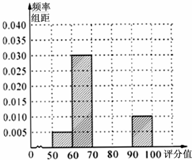 某单位进行了主题为“你幸福吗”的幸福指数问卷调查,得到每个调查对象的幸福指数评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表和频率分布直方图.
某单位进行了主题为“你幸福吗”的幸福指数问卷调查,得到每个调查对象的幸福指数评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表和频率分布直方图.| 幸福指数评分值 | 频数 | 频率 |
| [50,60] | ||
| (60,70] | ||
| (70,80] | ||
| (80,90] | 3 | |
| (90,100] | ||
| 合 计 | 20 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 6 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com