
【题目】如果函数![]() 在其定义域内存在实数
在其定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“可拆分函数”.
为“可拆分函数”.
(1)试判断函数![]() 是否为“可拆分函数”?并说明你的理由;
是否为“可拆分函数”?并说明你的理由;
(2)证明:函数![]() 为“可拆分函数”;
为“可拆分函数”;
(3)设函数![]() 为“可拆分函数”,求实数
为“可拆分函数”,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 不是“可分拆函数”(2)见解析(3)![]()
【解析】试题分析: (1)按照“可分拆函数”的概念,只需方程有根即可,据此判断;
(2)本问利用零点定理即可判断,即判断端点处的函数值异号即可证明结论;
(3)若函数在(0,+∞)上为可分拆函数,只需方程在该区间上有实根,然后借助于换元的方法,将![]() ,然后分离参数方法,即可求出
,然后分离参数方法,即可求出![]() 的取值范围.
的取值范围.
试题解析:
(1)假设![]() 是“可分拆函数”,则存在
是“可分拆函数”,则存在![]() ,使得
,使得![]()
即![]() ,而此方程的判别式
,而此方程的判别式![]() ,方程无实数解,
,方程无实数解,
所以,![]() 不是“可分拆函数”.
不是“可分拆函数”.
(2)令![]() ,
,
则![]() ,
,
又![]() 故
故![]() ,
,
所以![]() 在上有实数解
在上有实数解![]() ,也即存在实数
,也即存在实数![]() ,使得
,使得
![]() 成立,
成立,
所以![]() 是“可分拆函数”.
是“可分拆函数”.
(3)因为函数![]() 为“可分拆函数”,
为“可分拆函数”,
所以存在实数![]() ,使得
,使得![]() =
=![]() +
+![]() ,
,
![]() =
=![]() 且
且![]() ,所以
,所以![]() ,
,
![]() ,则
,则![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围是( )
A.![]()
B.k<0或![]()
C.![]()
D.![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,四棱锥P -ABCD的底面是矩形,侧面PAD是正三角形,
且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)求证:PB//平面EAC;
(2)求证:AE⊥平面PCD;
(3)当![]() 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图, 弧AC 长为 ![]() ,弧A1B1 长为
,弧A1B1 长为 ![]() ,其中B1与C在平面AA1O1O的同侧.
,其中B1与C在平面AA1O1O的同侧. 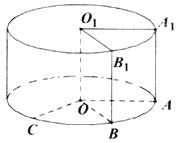
(1)求圆柱的体积与侧面积;
(2)求异面直线O1B1与OC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
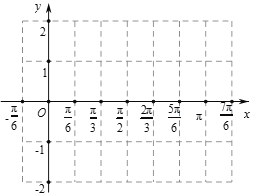
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() R,函数
R,函数 ![]() =
= ![]() .
.
(1)当 ![]() 时,解不等式
时,解不等式 ![]() >1;
>1;
(2)若关于 ![]() 的方程
的方程 ![]() +
+ ![]() =0的解集中恰有一个元素,求
=0的解集中恰有一个元素,求 ![]() 的值;
的值;
(3)设 ![]() >0,若对任意
>0,若对任意 ![]()
![]() ,函数
,函数 ![]() 在区间
在区间 ![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com