
分析 (1)由不等式的解集求出b、c的值,代入不等式bx2-(c+1)x-c>0求出解集A,
再根据交集的定义计算A∩B;
(2)利用基本不等式求$\frac{{{x^2}-3x+6}}{x-1}$的最小值即可.
解答 解:关于x的不等式x2-(b+2)x+c<0的解集为{x|2<x<3}
∴$\left\{\begin{array}{l}2+3=b+2\\ 2×3=c\end{array}\right.$,解得$\left\{\begin{array}{l}b=3\\ c=6\end{array}\right.$;
(1)不等式bx2-(c+1)x-c>0可化为3x2-7x-6>0,
由3x2-7x-6>0解得$x<-\frac{2}{3}$或x>3,
即$A=(-∞,-\frac{2}{3})∪(3,+∞)$;
又B=[-2,2),∴$A∩B=[-2,-\frac{2}{3})$;
(2)∵x>1,∴x-1>0,
则$\frac{{{x^2}-bx+c}}{x-1}=\frac{{{x^2}-3x+6}}{x-1}$
=$\frac{{{{(x-1)}^2}-(x-1)+4}}{x-1}$
=$(x-1)+\frac{4}{x-1}-1≥4-1=3$,
当且仅当x=3时等号成立,
即$\frac{{{x^2}-3x+6}}{x-1}$的最小值为3.
点评 本题考查了一元二次不等式与对应方程的关系和应用问题,也考查了基本不等式的应用问题,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (0,4) | C. | {0,1,2,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0) | B. | $(-3,-\frac{1}{2})$ | C. | (-3,-1) | D. | (-3,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{49}$ | B. | $\frac{4}{7}$ | C. | $\frac{25}{49}$ | D. | $\frac{51}{98}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
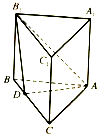 如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.
如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com