
分析 (Ⅰ)将x=4代入f(x)的解析式,解方程可得a的值;由绝对值的意义,讨论x的范围,运用二次函数的性质,可得单调区间;
(Ⅱ)作出f(x)的图象,考虑直线y=a与曲线有一个交点情况,即可得到所求a的范围.
解答 解:(Ⅰ)函数f(x)=x|m-x|,且f(4)=0.
得4|m-4|=0,解得m=4;
故f(x)=x|4-x|,
当x≥4时,f(x)=x2-4x=(x-2)2-4,
对称轴x=2在区间[4,+∞)的左边,
f(x)在[4,+∞)递增;
当x<4时,f(x)=x(4-x)=-(x-2)2+4,
可得f(x)在(-∞,2)递增;在(2,4)递减.
综上可得f(x)的递增区间为(-∞,2),(4,+∞);
递减区间(2,4);
(Ⅱ)画出函数f(x)的图象,如图所示: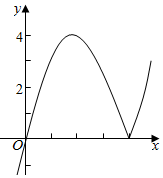
由f(x)的图象可知,
当a<0或a>4时,
f(x)的图象与直线y=a只有一个交点,
方程f(x)=a只有一个实根,
即a的取值范围是(-∞,0)∪(4,+∞).
点评 本题考查分段函数的运用:求单调区间,考查函数方程的转化思想,以及分类讨论的思想方法,注意数形结合的运用,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | f(a)>f(b)>f(c) | B. | f(a)>f(c)>f(b) | C. | f(c)>f(a)>f(b) | D. | f(c)>f(b)>f(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4•3n-1 | B. | 4•($\frac{3}{2}$)n-1 | C. | 4n | D. | 4•($\frac{5}{2}$)n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com