
分析 画出满足条件的平面区域,求出角点的坐标,结合函数图象求出z的最大值即可.
解答 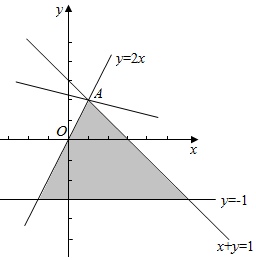 解:画出满足条件的平面区域,如图示:
解:画出满足条件的平面区域,如图示:
由$\left\{\begin{array}{l}{y=2x}\\{x+y=1}\end{array}\right.$,解得A($\frac{1}{3}$,$\frac{2}{3}$),
由z=x+3y得:y=-$\frac{1}{3}$x+$\frac{z}{3}$,
显然直线过A时,z最大,z的最大值是z=$\frac{1}{3}$+3×$\frac{2}{3}$=$\frac{7}{3}$,
故答案为:$\frac{7}{3}$.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100] |
| 甲班频数 | 5 | 6 | 4 | 4 | 1 |
| 乙班频数 | 1 | 3 | 6 | 5 | 5 |
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某小学对五年级的学生进行体质测试,已知五年级一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年级一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校高三年级800名学生在一次百米测试中,成绩全部介于13秒与18秒之间.抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部介于13秒与18秒之间.抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com