
 在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;
在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;分析 (Ⅰ)连结A1C∩AC1于F,则F为AC1的中点,连结DF,则A1B∥DF,由此能证明A1B∥平面AC1D.
(Ⅱ)过E作EM⊥AC于M,则EM⊥平面ABC,过M作MN⊥AD,垂足为N,连结EN,则∠ENM为二面角E-AD-C的一个平面角,由此利用二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$,能求出m的值.
解答 证明:(Ⅰ)连结A1C∩AC1于F,则F为AC1的中点,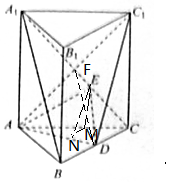
连结DF,则A1B∥DF,
∵DF?平面AC1D,∴A1B∥平面AC1D.
解:(Ⅱ)过E作EM⊥AC于M,则EM⊥平面ABC,过M作MN⊥AD,垂足为N,连结EN,
则EN⊥AD,∴∠ENM为二面角E-AD-C的一个平面角,
设EM=h,则$\frac{h}{3}$=$\frac{CM}{2}$,∴CM=$\frac{2h}{3}$,∴AM=2-$\frac{2h}{3}$,
∵$\frac{MN}{CD}=\frac{AM}{AC}$,∴MN=$\frac{AM}{AC}=1-\frac{h}{3}$,
∴EN2=EM2+MN2=h2+(1-$\frac{h}{3}$)2,
∵cos$∠ENM=\frac{\sqrt{10}}{10}$,故$\frac{(1-\frac{h}{3})^{2}}{{h}^{2}+(1-\frac{h}{3})^{2}}$=$\frac{1}{10}$,解得h=$\frac{3}{2}$,
此时,点E为A1C的中点,∴m=1.
点评 本题考查线面平行的证明,考查实数值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{3}{2}$ | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1,2} | B. | {-1,0,1} | C. | {-2,-1,0,1} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
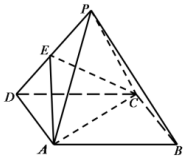 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com