
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
分析 (1)设高一女学生人数为x,由表1和2可得样本中男女生人数分别为40,30,则$\frac{700-x}{x}$=$\frac{40}{30}$,解得x.
(2)由表1和2可得样本中男女生人数分别为:5+14+13+6+3+1=42.样本容量为70.可得样本中该校学生身高在[165,180)的概率=$\frac{42}{70}$.即估计该校学生身高在[165,180)的概率.
(3)由题意可得:X的可能取值为0,1,2.由表格可知:女生身高在[165,180)的概率为$\frac{1}{3}$.男生身高在[165,180)的概率为$\frac{4}{5}$.即可得出X的分布列与数学期望.
解答 解:(1)设高一女学生人数为x,由表1和2可得样本中男女生人数分别为40,30,
则$\frac{700-x}{x}$=$\frac{40}{30}$,解得x=300.
因此高一女学生人数为300.
(2)由表1和2可得样本中男女生人数分别为:5+14+13+6+3+1=42.样本容量为70.
∴样本中该校学生身高在[165,180)的概率=$\frac{42}{70}$=$\frac{3}{5}$.
估计该校学生身高在[165,180)的概率=$\frac{3}{5}$.(3)由题意可得:X的可能取值为0,1,2.
由表格可知:女生身高在[165,180)的概率为$\frac{1}{3}$.男生身高在[165,180)的概率为$\frac{4}{5}$.
∴P(X=0)=$(1-\frac{4}{5})×(1-\frac{1}{3})$=$\frac{2}{15}$,P(X=1)=$\frac{4}{5}×(1-\frac{1}{3})$+$(1-\frac{4}{5})×\frac{1}{3}$=$\frac{9}{15}$,P(X=2)=$\frac{4}{5}×\frac{1}{3}$=$\frac{4}{15}$.
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{2}{15}$ | $\frac{9}{15}$ | $\frac{4}{15}$ |
点评 本题考查了频率与概率的关系、随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (2k-$\frac{2}{3}$,2k+$\frac{4}{3}$),k∈Z | B. | (2kπ-$\frac{2}{3}$π,2kπ+$\frac{4}{3}$π),k∈Z | ||
| C. | (4k-$\frac{2}{3}$,4k+$\frac{4}{3}$),k∈Z | D. | (4kπ-$\frac{2}{3}$π,4kπ+$\frac{4}{3}$π),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;
在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
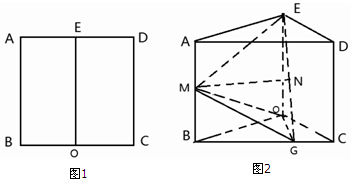
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1,2} | B. | {-1,-2} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com