
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,
,![]() 为上顶点,点
为上顶点,点![]() 为椭圆
为椭圆![]() 上一动点.
上一动点.
(1)若![]() ,求直线
,求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)设![]() 为椭圆
为椭圆![]() 的右焦点,过点
的右焦点,过点![]() 与
与![]() 轴垂直的直线为
轴垂直的直线为![]() ,
,![]() 的中点为
的中点为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 的交点在椭圆
的交点在椭圆![]() 上.
上.
【答案】(1)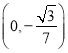 (2)见解析
(2)见解析
【解析】
(1)直接求出直线![]() 方程,与椭圆方程联立求出
方程,与椭圆方程联立求出![]() 点坐标,从而可得直线
点坐标,从而可得直线![]() 方程,得其与
方程,得其与![]() 轴交点坐标;
轴交点坐标;
(2)设![]() ,则
,则![]() ,求出直线
,求出直线![]() 和
和![]() 的方程,从而求得两直线的交点坐标,证明此交点在椭圆上,即此点坐标适合椭圆方程.代入验证即可.注意分
的方程,从而求得两直线的交点坐标,证明此交点在椭圆上,即此点坐标适合椭圆方程.代入验证即可.注意分![]() 和
和![]() 说明.
说明.
解:本题考查直线与椭圆的位置关系的综合,
(1)由题知![]() ,
,![]() ,则
,则![]() .因为
.因为![]() ,所以
,所以![]() ,
,
则直线![]() 的方程为
的方程为![]() ,联立
,联立 ,可得
,可得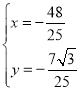
故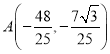 .则
.则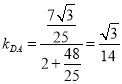 ,直线
,直线![]() 的方程为
的方程为![]() .令
.令![]() ,
,
得![]() ,故直线
,故直线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为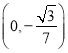 .
.
(2)证明:因为![]() ,
,![]() ,所以
,所以![]() .设点
.设点![]() ,则
,则![]() .
.
设
当![]() 时,设
时,设![]() ,则
,则![]() ,此时直线
,此时直线![]() 与
与![]() 轴垂直,
轴垂直,
其直线方程为![]() ,
,
直线![]() 的方程为
的方程为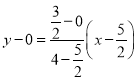 ,即
,即![]() .
.
在方程![]() 中,令
中,令![]() ,得
,得![]() ,得交点为
,得交点为![]() ,显然在椭圆
,显然在椭圆![]() 上.
上.
同理当![]() 时,交点也在椭圆
时,交点也在椭圆![]() 上.
上.
当![]() 时,可设直线
时,可设直线![]() 的方程为
的方程为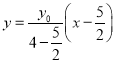 ,即
,即![]() .
.
直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程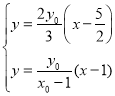 ,
,
消去![]() 得
得![]() ,化简并解得
,化简并解得![]() .
.
将![]() 代入
代入![]() 中,化简得
中,化简得![]() .
.
所以两直线的交点为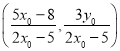 .
.
因为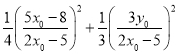
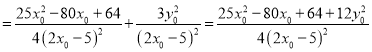 ,
,
又因为![]() ,所以
,所以![]() ,
,
则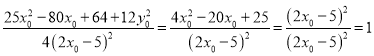 ,
,
所以点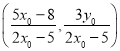 在椭圆
在椭圆![]() 上.
上.
综上所述,直线![]() 与直线
与直线![]() 的交点在椭圆
的交点在椭圆![]() 上.
上.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现对这两校参加考试的学生的数学成绩进行统计分析,数据统计显示,考生的数学成绩![]() 服从正态分布
服从正态分布![]() ,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
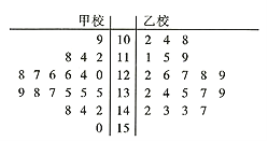
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
(3)从所有参加此次联考的学生中(人数很多)任意抽取3人,记数学成绩在134分以上的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
参考公式与临界值表:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 的棱长满足
的棱长满足![]() ,
,![]() ,现将四面体
,现将四面体![]() 放入一个主视图为等边三角形的圆锥中,使得四面体
放入一个主视图为等边三角形的圆锥中,使得四面体![]() 可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与x轴负半轴交于
与x轴负半轴交于![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的方程;
(2)设直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,连接AM,AN并延长交直线x=4于
两点,连接AM,AN并延长交直线x=4于![]() 两点,若
两点,若![]() ,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在![]() 内现将这100名学生的成绩按照
内现将这100名学生的成绩按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组后,得到的频率分布直方图如图所示,则下列说法正确的是
分组后,得到的频率分布直方图如图所示,则下列说法正确的是![]()
![]()

A. 频率分布直方图中a的值为![]()
B. 样本数据低于130分的频率为![]()
C. 总体的中位数![]() 保留1位小数
保留1位小数![]() 估计为
估计为![]() 分
分
D. 总体分布在![]() 的频数一定与总体分布在
的频数一定与总体分布在![]() 的频数相等
的频数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】詹姆斯·哈登(James Harden)是美国NBA当红球星,自2012年10月加盟休斯顿火箭队以来,逐渐成长为球队的领袖.2017-18赛季哈登当选常规赛MVP(最有价值球员).
年份 | 2012-13 | 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
常规赛场均得分y | 25.9 | 25.4 | 27.4 | 29.0 | 29.1 | 30.4 |
(Ⅰ)根据表中数据,求y关于t的线性回归方程![]() (
(![]() ,
,![]()
![]() *);
*);
(Ⅱ)根据线性回归方程预测哈登在2019-20赛季常规赛场均得分.
(附)对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:![]() ,
,![]()
(参考数据![]() ,计算结果保留小数点后一位)
,计算结果保留小数点后一位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接全国文明城市复检,绵阳某中学组织了本校1000名学生进行社会主义核心价值观、文明常识等内容测试。统计测试成绩数据得到如图所示的频率分布直方图,已知![]() ,满分100分.
,满分100分.
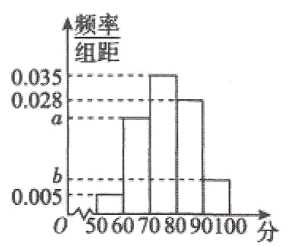
(1)求测试分数在![]() 的学生人数;
的学生人数;
(2)求这1000名学生测试成绩的平均数以及中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com