
����Ŀ�����й�ʽ����·�����ںܴ�Ľ�ͨ��ȫ������ij�������Ϊ�˽�·�˶ԡ��й�ʽ����·����̬���Ƿ����Ա��йأ�����·�������ȡ30��·�˽������ʾ����飬�õ���������������
��Ŀ | ���� | Ů�� | �ܼ� |
���� | 10 | ||
������ | 8 | ||
�ܼ� | 30 |
��֪����30���������ȡ1�˳鵽���С��й�ʽ����·����·�˵ĸ�����![]() .
.
(1)�뽫�������������������(ֱ��д���������Ҫд������)�����ݴ����Ϸ������С��й�ʽ����·�����Ա��Ƿ��йأ�
(2)������30���е�Ů��·���������ȡ2�˲μ�һ����Ƿ��С��й�ʽ����·��������ΪX����X�ķֲ��к���ѧ������
����K2��![]()
.
P(K2��k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
���𰸡���1��û�г����������Ϊ���С��й�ʽ����·�����Ա��йأ� ��2��![]() .
.
��������
![]() ���ݴ���30���������ȡ1�˳鵽���С��й�ʽ����·����·�˵ĸ��ʣ��������й�ʽ����·���������������ó���������������ñ����ٸ��������Ĺ�ʽ���
���ݴ���30���������ȡ1�˳鵽���С��й�ʽ����·����·�˵ĸ��ʣ��������й�ʽ����·���������������ó���������������ñ����ٸ��������Ĺ�ʽ���![]() ��ֵ��Ȼ�����ٽ�ֵ���Ƚϣ����ɵó�����
��ֵ��Ȼ�����ٽ�ֵ���Ƚϣ����ɵó�����
![]() X�Ŀ���ȡֵΪ0��1��2��ͨ���оٷ��õ��¼������ֱ��������ǵĸ��ʣ��г��ֲ��У����������
X�Ŀ���ȡֵΪ0��1��2��ͨ���оٷ��õ��¼������ֱ��������ǵĸ��ʣ��г��ֲ��У����������
(1)�������������£�
�Ա� | ���� | Ů�� | �ܼ� |
���� | 10 | 6 | 16 |
������ | 6 | 8 | 14 |
�ܼ� | 16 | 14 | 30 |
����֪���ݵ�K2�Ĺ۲�ֵK2��![]()
���ԣ�û�г����������Ϊ���С��й�ʽ����·�����Ա��йأ�
(2)X�Ŀ���ȡֵΪ0��1��2.
P(X��0)��![]() ��P(X��1)��
��P(X��1)��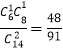 ��
��
P(X��2)��![]() ��
��
����X�ķֲ���Ϊ
X | 0 | 1 | 2 |
P |
|
|
|
X����ѧ����ΪE(X)��![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������P-ABC��,PA��ƽ��ABC,AB��AC,PA=AC=3,AB=![]() ,BE=
,BE=![]() EC,AD=2DC.
EC,AD=2DC.

(1)֤��:DE��ƽ��PAE;
(2)������A-PE-B������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC���ڽ�A��B��C���Եı߷ֱ���a��b��c����AB���ϵĸ�Ϊ ![]() ����a2+b2=2
����a2+b2=2 ![]() ab����C=�� ��
ab����C=�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA���ϱ������һ����·��OB�DZ�ƫ��45�㷽���һ����·��ij�羰����һ�α߽�Ϊ����C��Ϊ�����ο⣬�������C�ϵ�ij��ֱ����빫·OA��OB��ֱ��������·PM��PN����PM��PN����۷ֱ�Ϊ5��Ԫ/���ף�40��Ԫ/���ף�������ͼ��ʾ��ֱ������ϵxoy�������߷��Ϻ���y=x+ ![]() ��1��x��9��ģ�ͣ���PM=x����������·PM��PN�������Ϊf��x����Ԫ���������漰�ij��ȵ�λ��Ϊ���ף�
��1��x��9��ģ�ͣ���PM=x����������·PM��PN�������Ϊf��x����Ԫ���������漰�ij��ȵ�λ��Ϊ���ף�
��1����f��x������ʽ��
��2����xΪ����ʱ�������f��x����ͣ�����������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABC��A1B1C1�У������ABC��ֱ�������Σ�AB=AC=1����P����BB1��һ�㣬���� ![]() ��0�ܦˡ�1����
��0�ܦˡ�1���� 
��1������= ![]() ����ֱ��PC��ƽ��A1BC���ɽǵ�����ֵ��
����ֱ��PC��ƽ��A1BC���ɽǵ�����ֵ��
��2���������P��A1C��B������ֵΪ ![]() ����˵�ֵ��
����˵�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ϊ��ĵȲ�����{an}�У� S2��16����![]() �ɵȱ�����.
�ɵȱ�����.
��1��������{an}��ͨ�ʽ��
��2��������{|an|}��ǰn���Tn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����C��һ��������������C1:y2=-16x�Ľ����غ�,����������Ϊ2.
(1)��˫����C�ķ���;
(2)��˫����C�Ľ�������������C1������Χ�������ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ��ֳ������ijˮ��Ʒ���¡���������ֳ�����IJ����Աȣ��ջ�ʱ�������ȡ��100�����䣬��������ˮ��Ʒ�IJ�������λ��kg��, ��Ƶ�ʷֲ�ֱ��ͼ���£�

��1����A��ʾ�¼�������ֳ�������������50 kg��������A�ĸ��ʣ�
��2����д�������������������������ж��Ƿ���99%�İ�����Ϊ���������ֳ�����йأ�
�������50 kg | �������50 kg | |
����ֳ�� | ||
����ֳ�� |
��3�������������Ƶ�ʷֲ�ֱ��ͼ������������ֳ���������ӽ��бȽ�.
����
P�� | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABC-A1B1C1�У�![]() ��
��![]() ��E����CC1�е㣬F��AB���е�.
��E����CC1�е㣬F��AB���е�.
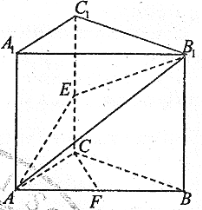
��1����֤��CF//ƽ��AEB1��
��2�����B��ƽ��AEB1�ľ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com