
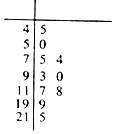
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.分析 (1)利用茎叶图性质和等可能事件概率计算公式能求出该样本中空气质量优良的频率,从而能估计该月空气质量优良的天数.
(2)该样本中空气质量不佳共4天,利用对立事件概率计算公式能求出该两天的空气质量等级恰好不同的概率.
解答 解:(1)从茎叶图中可发现该样本中空气质量优的天数为2,
空气质量良的天数为4,
故该样本中空气质量优良的频率为$\frac{6}{10}=\frac{3}{5}$,
从而估计该月空气质量优良的天数为$30×\frac{3}{5}=18$
(2)该样本中空气质量不佳共4天,
所以该两天的空气质量等级恰好不同的概率为$1-\frac{1}{C_4^2}=\frac{5}{6}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲是乙的充分条件但不是必要条件 | |
| B. | 甲是乙的必要条件但不是充分条件 | |
| C. | 甲是乙的充要条件 | |
| D. | 甲既不是乙的充分条件也不是乙的必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“¬p∧q”是真命题 | B. | 命题“p∧¬q”是真命题 | ||
| C. | 命题“p∧q”是真命题 | D. | 命题“¬p∨¬q”是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | [0,2] | C. | [1,2) | D. | [1,$\sqrt{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com