电视传媒公司为了解某地区观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．下面是根据
调查结果绘制的
观众日均收看该体育节目时间的频率分布直方图：
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性．
(1)根据已知条件完成下面的2×2列联表，并据此资料你是否认为“体育迷”与性别有关？
|
| 非体育迷 | 体育迷 | 合计 |
| 男 | |||
| 女 | |||
| 合计 |
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率．
附：χ2＝
，
| P(χ2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
名校课堂系列答案科目：高中数学 来源： 题型：
某班有50个同学，其中男生30人，女生20人，某次导师要抽5位同学打扫卫生，依性别按人数作分层抽样，则班上的男同学甲被抽中的概率是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
甲、乙两药厂生产同一型号药品，在某次质量检测中，两厂各有5份样品送检，检测的平均得分相等(检测满分为100分，得分高低反映
该样品综合质量的高低)．成绩统计用茎叶图表示如图：
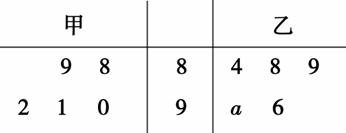
(1)求a；
(2)某医院计划采购一批该型号药品，从质量的稳定性角度考虑，你认为采购哪个药厂的产品比较合适？
(3)检测单位从甲厂送检的样品中任取两份作进一步分析，在抽取的两份样品中，求至少有一份得分在(90,100]之间的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
为了调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了200位老年人，结果如下：
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 70 | 40 |
| 不需要 | 30 | 60 |
附表：
| P(K2＞k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
K2＝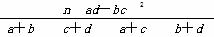
参照附表，得到的正确结论是( )
A．在犯错误的概率不超过0.1%的前提下，认为“该地区的老年人是否需要志愿者提供帮助与性别有关”
B．在犯错误的概率不超过0.1%的前提下，认为“该地区的老年人是否需要志愿者提供帮助与性别无关”
C．最多有99%的把握认为“该地区的老年人是否需要志愿者提供帮助与性别有关”
D．最多有99%的把握认为“该地区的老年人是否需要志愿者提供帮助与性别无关”
查看答案和解析>>
科目：高中数学 来源： 题型：
如图，若依次输入的x分别为
π，
，相应输出的y分别为y1，y2，则y1，y2的大小关系是( )
A．y1＝y2 B．y1>y2
C．y1<y2 D．无法确定
查看答案和解析>>
科目：高中数学 来源： 题型：
已知某算法的流程图如图所示，若将输出的(x，y)值依次记为(x1，y1)，(x2，y2)，
…，(xn，yn)，…
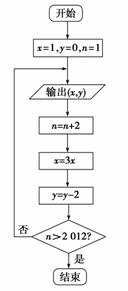
(1)若程序运行中输出的某个数组是
(t，－6)，则t＝________________；
(2)程序结束时，共输出(x，y)的组数为__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
设点A,B的坐标分别为
,
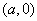.直线AM,BM相交于点M，且他们的斜率之积为
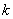.则下列说法正确的是________
（1）当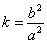
时，点M的轨迹是双曲线，（其中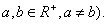
（2）当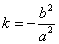
时，点M的轨迹是部分椭圆，（其中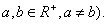
（3）在（1）的条件下，点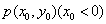
是曲线上的点。
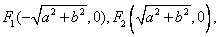且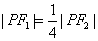
，则（1）的轨迹所在的圆锥曲线的离心率取值范围为
（4）在（2）的条件下，过点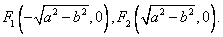
满足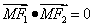
的点M总在曲线的内部，则（2）的轨迹所在的圆锥曲线的离心率的取值范围是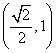
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，已知点
在圆
内，动直线
过点
且交圆
于
两点，若△ABC的面积的最大值为
，则实数
的取值范围为 ．