考点:用空间向量求平面间的夹角,直线与平面垂直的性质,二面角的平面角及求法
专题:空间角
分析:(1)根据线面垂直的性质先证明AC⊥平面ABB1A1,即可证明AC⊥BB1;
(2)建立空间直角坐标系,求出平面的法向量,利用向量法即可得到结论.
解答:
解:(1)在三棱柱ABC-A
1B
1C
1中,因为A
1B⊥平面ABC,A
1B?平面ABB
1A
1,
所以平面ABB
1A
1⊥平面ABC,
因为平面ABB
1A
1∩平面ABC=AB,AB⊥AC,
所以AC⊥平面ABB
1A
1,所以AC⊥BB
1.
(2)如图,建立以A为原点的空间直角坐标系,
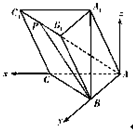
则C(2,0,0),B(0,2,0),A
1(0,2,2),B
1(0,4,2),
则
==(2,-2,0),
设
=λ=(2λ,-2λ,0),λ∈[0,1],
则P(2λ,4-2λ,2),
设平面PAB的一个法向量为
=(x,y,z),
因为
=(2λ, 4-2λ, 2),
=(0, 2, 0),
,
即
,所以
,
令x=1得
=(1,0,-λ),
而平面ABA
1的一个法向量是
=(1,0,0),
则|cos<
,
>|
=
=,
解得
λ=,即P为棱B
1C
1的中点.
点评:本题主要考查线面垂直的判断和性质,以及二面角的应用,建立空间直角坐标系利用向量法是解决本题的关键.

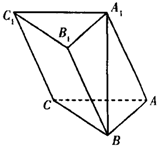 如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC. 则C(2,0,0),B(0,2,0),A1(0,2,2),B1(0,4,2),
则C(2,0,0),B(0,2,0),A1(0,2,2),B1(0,4,2),

 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.