
(本小题满分12分)
已知奇函数 在
在 上有意义,且在(
上有意义,且在( )上是增函数,
)上是增函数, ,又有函数
,又有函数 ,若集合
,若集合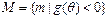 ,集合
,集合
 (1)求
(1)求 的解集;
的解集;
(2)求 中m的取值范围
中m的取值范围
(1)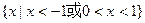
(2)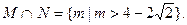
解析解:(1)
 为奇函数且
为奇函数且
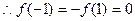
又 在(1,+
在(1,+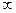 )上是增函数
)上是增函数 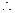
 在(-
在(-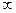 ,0)上也是增函数
,0)上也是增函数
故 的解集为
的解集为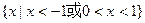 -------------------------------------3分
-------------------------------------3分
(II)由(1)知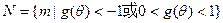
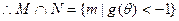 ----------------------------------------------------------5分
----------------------------------------------------------5分
由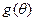 <-1得
<-1得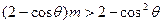 -----------------------------------------7分
-----------------------------------------7分
即 --------------------------------9分
--------------------------------9分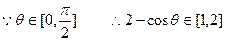
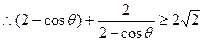 ,等号成立时
,等号成立时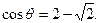
故4-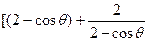 ]的最大值是
]的最大值是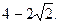 -----------------------------11分
-----------------------------11分
从而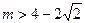 ,即
,即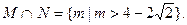 ---------------------------12分
---------------------------12分


科目:高中数学 来源: 题型:解答题
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作 横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
2010年推出一种新型家用轿车,购买时费用为14.4万元,每年应交付保险费.养路费及汽油费共0.7万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(1)设该辆轿车使用n年的总费用(包括购买费用.保险费.养路费.汽油费及维修费)为f(n),求f(n)的表达式;
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
已知函数f(x)=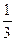 x
x -(2a+1)
-(2a+1) x
x +3a(a+2)x+
+3a(a+2)x+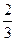 ,其中a为实数。
,其中a为实数。
(1)当a=-1时,求函数y=f(x)在[0,6]上的最大值与最小值;
(2)当函数y=f (x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数 在其定义域上满足
在其定义域上满足 .
.
(1)函数 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当 时,求x的取值范围;
时,求x的取值范围;
(3)若 ,数列
,数列 满足
满足 ,那么:
,那么:
①若 ,正整数N满足
,正整数N满足 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列 ,
,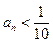 恒成立,求最小的N;
恒成立,求最小的N;
②若 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
小刘家要建造一个长方形无盖蓄水池,其容积为48 ,深为3
,深为3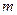 .如果池底每平方米的造价为150元,池壁每平方米的造价为
.如果池底每平方米的造价为150元,池壁每平方米的造价为 120元,怎样设计水池能使总造价最低?最低造价是多少?
120元,怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com