练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．计算：${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx=$\sqrt{3}$+$\frac{2π}{3}$．

    分析 ${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx表示如图阴影部分的面积，而S阴影=2S△ABC+S扇形CAD，解得即可．

    解答 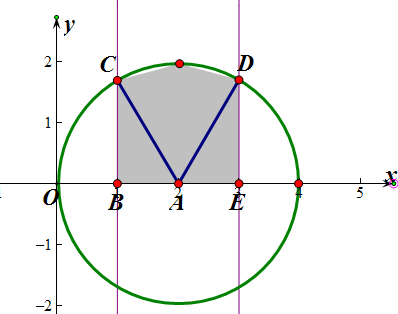解：令$\sqrt{4-（x-2）^{2}}$=y，y≥0，
    ∴（x-2）2+y2=4，
    则${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx表示如图阴影部分的面积，
    ∴S阴影=2S△ABC+S扇形CAD=2×$\frac{1}{2}$×1×$\sqrt{3}$+$\frac{1}{6}$π×4=$\sqrt{3}$+$\frac{2π}{3}$，
    ∴${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx=$\sqrt{3}$+$\frac{2π}{3}$，
    故答案为：$\sqrt{3}$+$\frac{2π}{3}$

    点评 本题主要考查积分的几何意义，熟练掌握微积分基本定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．设向量$\overrightarrow{OA}$=（a，cos2x），$\overrightarrow{OB}$=（1+sin2x，1），x∈R，函数f（x）=$|\begin{array}{l}{\overrightarrow{OA}}\\{\;}\end{array}|$•$|\begin{array}{l}{\overrightarrow{OB}}\\{\;}\end{array}|$cos∠AOB
    （Ⅰ）当y=f（x）的图象经过点（$\frac{π}{4}$，2）时，求实数a的值；
    （Ⅱ）在（Ⅰ）的条件下，若x为锐角，当sin2x=sin（$\frac{π}{4}$+α）•sin（$\frac{π}{4}$-α）+$\frac{1-cos2α}{2}$时，求△OAB的面积；
    （Ⅲ）在（Ⅰ）的条件下，记函数h（x）=f（x+t）（其中实数t为常数，且0＜t＜π）．若h（x）是偶函数，求t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若a，b，c∈（0，+∞），且a+b+c=1，则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值为（　　）
    A．$\frac{1}{3}$B．$\frac{\root{3}{2}}{3}$C．$\frac{9}{2}$D．$\frac{1}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．$cos（\frac{19π}{3}）$的值为（　　）
    A．$\frac{1}{2}$B．$\frac{{\sqrt{3}}}{2}$C．$-\frac{1}{2}$D．$-\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．（1）已知角α的终边上一点P（-4，3），求$\frac{cos（\frac{π}{2}+α）sin（π-α）}{cos（\frac{11π}{2}-α）sin（\frac{9π}{2}+α）}$的值．
    （2）已知tanα=2，求$\frac{sinα-cosα}{3sinα+2cosα}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知△ABC的三边满足（a+b+c）（a+b-c）=（$\sqrt{3}$+2）ab，则角C等于（　　）
    A．15°B．30°C．45°D．60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

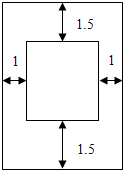    1．某出版社出版一读物，为了排版设计的需要，规定：一页上所印文字的矩形区域需要占去150cm2，上、下边各要留1.5cm宽的空白，左、右两边各要留1cm宽的空白，出版商为了节约纸张，应选用怎样尺寸的矩形纸张来设计版面？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．记函数f（x）=$\sqrt{（x+1）（x-1）}$的定义域为A，函数g（x）=lg[（x-a-1）（2a-x）]（a＜1）的定义域为B
    （1）求A、B； 
    （2）若B⊆A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在三角形ABC中，点D是线段BC中点，点F在线段CD上，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，z=$\frac{1}{x}$+$\frac{4}{y}$，若$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$，求z最小值．

    查看答案和解析>>

    同步练习册答案